大佬Steinke讲CDP的视频,https://www.youtube.com/watch?v=U2PoAi5WHLM。看了记录下。
-
Why need a new definition?
Puer-DP is mathematically elegant, but too restrictive in mayn settings.
可能在小概率事件上卡住?
组合性质比它应该能达到性能quadratically worse.
Approximate-DP is more permissive, it has better privacy-utility tradeoff.
可以忽略概率小于等于$\delta$的事件;
对于high level的组合性可以得到更好的bounds;
However, mathematically inelegant. key composition property is very messy.
Doesn’t sharply capture what’s going on. Pay $\log(\frac{1}{\delta})$ factors in analysis.
所以,是否有两全的办法?
- 组合性质

大佬在这里说,sorry, it is not very intuitive..
-
Composition for $(\varepsilon,\delta)$-DP is not “associative”.
举例子,四个不同的随机算法组合在一起和四个不同的随机算法两两组合然后再组合,是不一样的。
End up paying a $\sqrt{\log(\frac{1}{\delta})}$ factor for each level of composition
-
CDP的组合性


- 标准CDP算法


- Understanding Concentrated DP


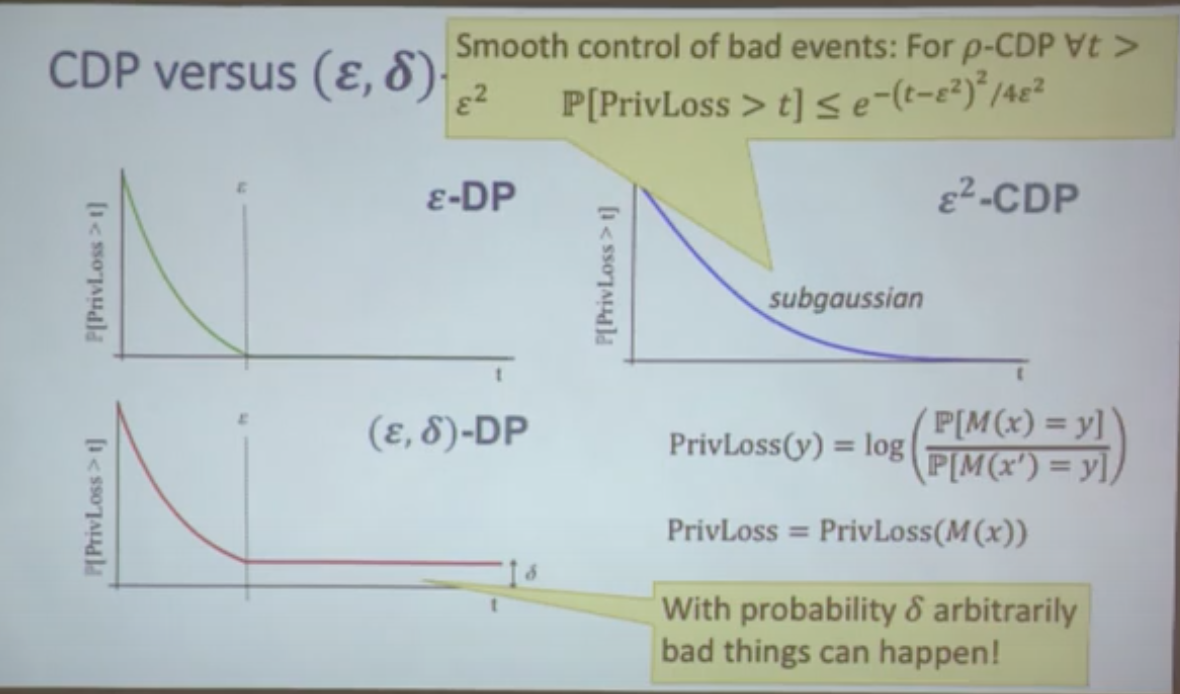
$PrivLoss\sim N(\varepsilon^2,2\varepsilon^2)$
矩生成函数$\mathbb{E}[e^{(\alpha-1)PirvLoss}] \leq e^{\alpha(\alpha-1)\varepsilon^2}$,这个和$\varepsilon^2$-CDP是等价的。

完全没懂。。

CDP是介于pure-DP和approximate-DP之间的,但是又拥有advanced composition等特性,可以通过高斯机制实现。(是说通过更少的噪声实现同样的保护吗?)
- Limitations





结论
不是很懂!
