Blondel M, Fujino A, Ueda N. Convex factorization machines[C]//Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer, Cham, 2015: 19-35.
FM结合了特征工程,因此取得了不错的效果。但是,FM涉及到了非凸优化问题,可能收敛到不太好的局部极值点上。本文基于核范数提出了FM的凸表达式。这种表达对于模型的限制更小,因此比原来的表达更为通用。为了解决对应的优化问题,本文提出了有效的globally-convergent two-block coordinate descent algorithm。在四个推荐任务上表现的都和原始表达式差不都或者更好,并且扩展到了千万级的数据上。
Introduction
FM将交互矩阵Z分解成$VV^T$,其中$V\in R^{d\times k}, k«d$,这样减少了过拟合的风险,因为参数的数量级从$d^2$降到了$kd$个。FM可以通过选择不同的特征表达,来模拟许多已有的分解模型,比如标准的矩阵分解、SVD++、timeSVD++和PITF等。但是有两个缺点,一是涉及到了非凸优化问题;二是需要选择一个合适的超参数k。
本文提出的基于核范数的FM的凸表达式,由于对交互矩阵的限制更少,因此比原来的FM表达式更通用。不需要选择超参数k。

Convex Formulation
首先将原先的预测式重写:
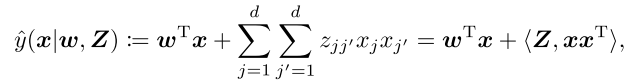
为了降低矩阵Z的$O(d^2)$的复杂度,本文学习了低秩矩阵Z,$rank(Z) \ll d$。通过regularizing Z with the nuclear norm,核范数是矩阵秩的最紧的凸下界。对于对称矩阵Z,核范数定义为:
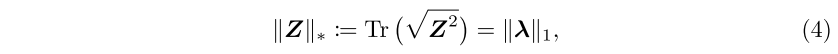
$\lambda$是集合了Z的特征值的向量。对z用核范数进行正则化,和对它的特征值进行L1范数的正则化,二者是等价的,后者会促进稀疏性。由于$rank(Z)=\Vert \lambda \Vert_0 = \vert supp(\lambda)\vert$,因此核范数也可以促进低秩。于是,将FM重写为如下优化问题:
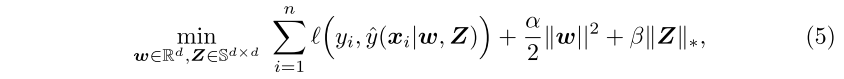
其中,l是二次可微凸函数,$\alpha,\beta>0$是超参数。(5)是jointly convex in w and Z,这个式子不需要超参数k。Z的秩由$\beta$间接控制,$\beta$越大,Z的秩越小。
对称矩阵可以对角化,因此预测式可以重写为:
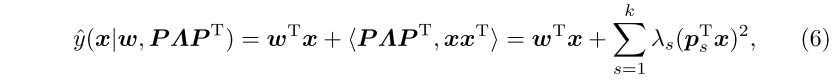
其中$k=rank(Z)$。
Optimization Algorithm
为了求解(5),提出一种two-block coordinate descent algorithm,对w和Z交替进行最小化直到收敛。
Minimizing with respect to w
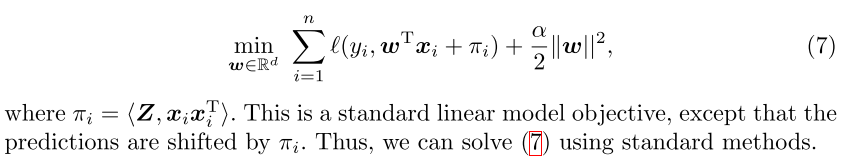
Minizing with respect to Z
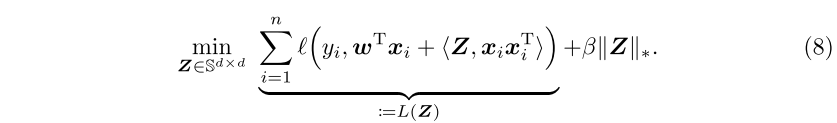
解决核范数正则化问题的两种方法是近似梯度(proximal gradient)和ADMM。这类方法的关键是近似操作,需要SVD,在扩展到大规模数据时会成为瓶颈。因此,本文采用贪心的坐标下降算法来解决这一问题。本文算法的主要区别是,利用了Z的对称性,学习Z的特征分解而不是SVD。
Experiments