Wang D, Chen C, Xu J. Differentially private empirical risk minimization with non-convex loss functions[C]//International Conference on Machine Learning. 2019: 6526-6535.
本文研究了DP-ERM with (smooth) non-convex loss function问题。我们首先研究预期的过量经验(或总体)风险,该风险主要用作衡量凸损失函数质量的工具。
We first study the expected excess empirical (or population) risk, which was primarily used as the utility to measure the quality for convex loss functions.
在$(\epsilon,\delta)$-DP中,上述risk的上界是$\tilde{O}(\frac{d \log(1/\delta)}{\log n\epsilon^2})$,n是数据总数,d是空间的维度。通过对时间平均误差的高度平凡的分析,$\frac{1}{\log n}$项可以进一步提高到$\frac{1}{n^{\Omega(1)}}$(当d维常数的时候)。
为了得到更有效的解决方案,考虑了DP和近似local最小值的联系。特别地,当n足够大时,存在$(\epsilon,\delta)$-DP算法,可以在约束和非约束条件下大概率找到经验风险的近似局部最小值。
Introduction
之前DP-ERM的工作关注的都是凸的损失函数,但是,非凸的损失函数在实际中会得到更好的分类准确性。研究非凸的并不多[1,2,3],可能是因为找到非凸损失函数的全局最小值是一个NP难的问题。工作[1,2,3]用梯度的l2-norm来衡量error bound。这样做的一些缺点是:
- 尽管[1,2,3]表明,随着n趋向无穷,梯度的norm趋近于0,但是并不能保证estimator可以接近非退化的局部最小值[4](non-degenerate local minimum);
- 梯度范数的estimator不总和损失函数的excess empirical risk保持一致。
1) although (Zhang et al., 2017; Wang et al., 2017; Wang & Xu, 2019) showed that the gradient norm tends to 0 as n goes to infinity, there is no guarantee that such an estimator will be close to any non-degenerate local minimum (Agarwal et al., 2017); 2) the gradient-norm estimator is not always consistent with the excess empirical (population) risk of the loss function, i.e.,$\hat{L}(w^{priv})-\hat{L}(w^)$, where $w^$ is the optimal solution (Bassily et al., 2014; Chaudhuri et al., 2011).
因此,很难将获得的解与全局或局部最小值进行比较。于是,本文提出以下问题:
- excess empirical (population) risk是否可以用来衡量DP条件下,非凸损失函数的error bound?
由于深度学习中,找到一个全局最小值是很难的,很多机器学习的工作开始将注意力转移到寻找局部最小值上。已有工作表明,快速收敛到局部最小值对于这些任务来说已经足够了,但是收敛到临界点(critical points, 梯度消失的点)是不可接受的。[5]表明,为非凸函数计算局部最小值实际上是NP-hard的。幸运的是,机器学习中的许多非凸函数都是严格的鞍[6],这意味着二阶固定点(或近似局部最小值)足以获得足够接近一些局部最小值的点。
为了找到(近似的)局部最小值,[6]提出用噪声扰动梯度的方法,即在每次更新参数前的迭代中加入一定量的高斯噪声。而这正好和DP社区的方案很像。尽管两种方案出发点不同(一个是为了逃离鞍点,另一个是为了使算法满足DP),但是都在迭代过程中为梯度加入了高斯噪声。很自然提出另一个问题:
- 是否可以找到一些近似局部最小值,既可以逃离鞍点,又可以保证DP?
本文的主要贡献就是回答上述两个问题,并给出肯定回答。
对第一个问题,提出了DP-GLD,证明了当$\log n\ge O(d)$时,excess empirical risk的上界是$\tilde{O}(\frac{d \log(1/\delta)}{\log n\epsilon^2})$,n是数据数量,d是空间的维度。采用的技术是基于最近在Bayesian learning and (stochastic) Gradient Langevin Dynamiscs上的一些工作[7-10]。
对第二个问题,当n足够大时,存在多项式时间的$(\epsilon,\delta)$-DP算法,可以在约束和非约束条件下找到经验风险的近似局部最小值($\alpha$-approximate local minimum of the empirical risk in both constrained and non-constrained settings)。是第一个将DP和逃离鞍点联系起来的工作。
Related Work
对于DP-ERM with convex loss functions,已经有很多工作了,
-
比如Chaudhuri大佬的开篇之作(09nips 11jmlr),
Bassily, R., Smith, A., and Thakurta, A. Private empirical risk minimization: Efficient algorithms and tight error bounds. In Foundations of Computer Science (FOCS), 2014 IEEE 55th Annual Symposium on, pp. 464–473. IEEE, 2014.
[1,2]
Kifer, D., Smith, A., and Thakurta, A. Private convex empirical risk minimization and high-dimensional regression. In Conference on Learning Theory, 2012.等。
-
还有考虑高维的,
Talwar, K., Thakurta, A. G., and Zhang, L. Nearly optimal private lasso. In Advances in Neural Information Processing Systems, pp. 3025–3033, 2015.
Talwar, K., Thakurta, A., and Zhang, L. Private empirical risk minimization beyond the worst case: The effect of the constraint set geometry. arXiv preprint arXiv:1411.5417, 2014.
Kasiviswanathan, S. P. and Jin, H. Efficient private em- pirical risk minimization for high-dimensional learning. In International Conference on Machine Learning, pp. 488–497, 2016.
-
还有考虑ERM in the non-interactive local model的,
Wang, D., Gaboardi, M., and Xu, J. Empirical risk mini- mization in non-interactive local differential privacy revis- ited. Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Process- ing Systems 2018, 3-8 December 2018, Montreal, QC, Canada, 2018.
Wang, D., Smith, A., and Xu, J. Noninteractive locally private learning of linear models via polynomial approxi- mations. In Algorithmic Learning Theory, pp. 897–902, 2019.
对于非凸损失函数,已有的工作主要采用梯度norm作为衡量来bound private estimator的误差[1,2,3]。由于梯度范数通常不能保证解的质量,因此将这些界限与本文中的界限进行比较不是很有意义。[2]对于某些满足Polyak-Lojasiewicz条件的非凸损失函数,给出了近似最优的界。
[Balcan, M.-F., Dick, T., and Vitercik, E. Dispersion for data-driven algorithm design, online learning, and private optimization. In 2018 IEEE 59th Annual Symposium on Foundations ofComputer Science (FOCS), pp. 603–614. IEEE, 2018.] studied the problem of optimizing privately piecewise Lipschitz functions in online settings. 这篇文章的损失函数要满足dispersion条件,和本文很不同,也不能比较。
[Wang, Y.-X., Fienberg, S., and Smola, A. Privacy for free: Posterior sampling and stochastic gradient monte carlo. In International Conference on Machine Learning, 2015.]
[Li, B., Chen, C., Liu, H., and Carin, L. On connecting stochastic gradient mcmc and differential privacy. In Chaudhuri, K. and Sugiyama, M. (eds.), Proceedings of Machine Learning Research, volume 89, pp. 557–566, 2019.]
上述这俩工作搞了个DP版本的SGLD,关注的是Bayesian learning,和本文也不一样。
本文的工作主要关注在非凸损失函数上的DP-ERM问题,和private estimator对于全局或局部最小值的误差。其次,现有的工作需要假设在gradient Langevin dynamics中,温度参数是常数,而本文并没有这样的假设,所以比之前的工作更具有挑战性。
####Preliminaries

还有一些如Lipschitz条件,光滑函数,Moments Accountant,高斯机制指数机制等基础知识就不列出了,有需要可以参考论文。

Excess Risk of DP-ERM with Non-convex Loss Functions
做了一些假设,这些假设在DP-ERM with convex loss functions中很常见:
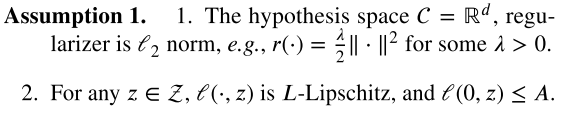
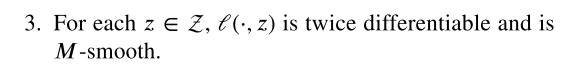
Gradient Langevin Dynamics (GLD)算法,梯度下降算法等一种泛化:在第k次迭代时,

它可以被看作是连续时间Langevin扩散的离散时间近似值,由以下随机微分方程(SDE)描述:

有工作表明(2)中扩散过程的分布会收敛于它的固定分布。当$\beta\to\infin$时,分布会集中在$\hat{L}^r(w,D)$的最小值周围。通过合理的选择步长$\eta$,GLD可以满足DP。如算法1。

接下来的定理1证明了算法1满足DP。定理2给出了population risk和empirical risk的理论上界。(这里有几个地方看不明白,1. 什么是the probability law,用在Wasserstein distance里的;)
接下来说定理2给出的经验风险只在$\beta \ge O(d)$的时候才有意义。bound比凸损失函数的情况大。于是定理3利用随机微分方程2给出了改进的bound。
Theorem 3 is a significant improvement over Theorem 2, which is derived based on a novel and non-trivial analysis on the time-average error of SDEs.
有三点值得强调:1)虽然time-average-error analysis of an SDE已经被研究过了,但是之前的文章中$\beta$是常数,不能直接应用到本文。之前的工作需要假设基于泊松方程解的有界假设,对于本文来说太强了。2)本文结果意义重大,因为它为基于扩散的贝叶斯采样提供了新的界限,例如(Vollmer等,2016; Chen等,2015),其中可以量化误差范围内对d的依赖性, 是先前结果中缺少的关键片段。3)定理3表明,如果返回随机的$w_j$而不是最终的$w_T$,和n相关的项可以从$1/\log n$变为$n^{-\tau}$. (每个字都能看懂,连起来就有点懵逼)
接下来的定理4表明,在假设1的情况下,存在$\epsilon$-DP算法,经验风险的bound是$\tilde{O}(\frac{d}{n\epsilon})$,时间复杂度是指数级的(这还能用吗)。考虑d是常数,
对于population risk的上界,针对具体问题来改进bound。主要关注generalized linear model with non-convex loss functions and the robust regressions problem with additional assumptions,提出了population risk是$O(\frac{\sqrt[4]{d}}{\sqrt{n\epsilon}})$。
Generalized Linear Model (GLM).
| $\mathcal{X}={x\in\mathbb{R}^d | \Vert x\Vert_2\leq 1}, C={w\in\mathbb{R}^d | \Vert w\Vert_2\leq 1}, and\ \mathcal{Y}={0,1},\ \mathcal{Z}=\mathcal{X}\times\mathcal{Y}$,同时有一个link function $\sigma$,GLM拥有损失函数:$\mathcal{l}(w,(x,y))=(\sigma(\langle w,x\rangle)-y)^2$。 |
随后定义了Robust Regression:
令$\mathcal{Z}$和$C$一样,对于常数Y来说,$\mathcal{Y}=[-Y,Y]$,对非凸的正损失函数$\psi$,定义loss of robust regression as $l(w,(x,y))=\psi(\langle x,w \rangle -y)$。(这个是不是写错了?)

算法2是基于Frank-wolfe方法来的。定理5给出了在GLM和Robust Regression情况下的bound of the population risk的上界是$O(\frac{\sqrt[4]{d\ln \frac{1}{\delta}}}{\sqrt{n\epsilon}})$。
| 被算法2启发,在条件成为$\mathcal{X}={x\in\mathbb{R}^d | \Vert x\Vert_\infin\leq 1}, C={w\in\mathbb{R}^d | \Vert w\Vert_1\leq 1}$时,可以推导出population risk的上界只依赖于$\log d$,表明适用于高维数据的应用。直接用(Talwar, K, 2015)提出的DP-Frank-Wolfe算法来解决我们的问题。 |
定理6给出了算法3的bound。

Finding Approximate Local Minimum Privately
Reference
[1] Zhang, J., Zheng, K., Mou, W., and Wang, L. Efficient private erm for smooth objectives. In Proceedings ofthe 26th International Joint Conference on Artificial Intelligence, pp. 3922–3928. AAAI Press, 2017.
[2] Wang, D., Ye, M., and Xu, J. Differentially private empirical risk minimization revisited: Faster and more general. In Advances in Neural Information Processing Systems, 2017.
[3] Wang, D., Smith, A., and Xu, J. Noninteractive locally private learning of linear models via polynomial approximations. In Algorithmic Learning Theory, pp. 897–902, 2019.
[4] Agarwal, N., Allen-Zhu, Z., Bullins, B., Hazan, E., and Ma, T. Finding approximate local minima faster than gradient descent. In Proceedings of the 49th Annual ACM SIGACTSymposium on Theory ofComputing, pp. 1195–1199. ACM, 2017.
[5] Anandkumar, A. and Ge, R. Efficient approaches for escap- ing higher order saddle points in non-convex optimization. In Conference on Learning Theory, pp. 81–102, 2016.
[6] Ge, R., Huang, F., Jin, C., and Yuan, Y. Escaping from saddle points-online stochastic gradient for tensor decomposition. In Conference on Learning Theory, pp. 797–842, 2015.
[7] Raginsky, M., Rakhlin, A., and Telgarsky, M. Non-convex learning via stochastic gradient langevin dynamics: a nonasymptotic analysis. In Proceedings ofthe 2017 Conference on Learning Theory, 2017.
[8] Chen, C., Ding, N., and Carin, L. On the convergence of stochastic gradient mcmc algorithms with high-order in- tegrators. In Advances in Neural Information Processing Systems, 2015.
[9] Xu, P., Chen, J., Zou, D., and Gu, Q. Global convergence of langevin dynamics based algorithms for nonconvex opti- mization. In Advances in Neural Information Processing Systems, pp. 3126–3137, 2018a.
[10] Tzen, B., Liang, T., and Raginsky, M. Local optimality and generalization guarantees for the langevin algorithm via empirical metastability. In Conference On Learning Theory, pp. 857–875, 2018.
