IEEE Symposium on Security and Privacy 2019
Abstract
之前提出的基于DP的用来解决凸优化问题的算法都不能部署到实践中。本文提出了Approximate Minima Pertubation,可以针对当前的任何优化器实现隐私保护算法,并且不需要超参数的调整;其次做了一些评估比较,和当前的DP凸优化方法进行了比较;最后给出了开源实现。
Introduction
本文的目标是基于目标扰动的方式对实际的(practical)DP凸优化问题进行深入了解,主要的技术贡献是设计了一种新的隐私保护凸优化算法,该算法适用于现实情况,并提供隐私和实用性保证。
Objective Perturbation针对目标函数进行扰动,然后计算新的最小值。然而,这种方法只有在可以求得perturbed objective的精确最小值的条件下才能保证隐私。实践中,解决凸优化经常引入一阶迭代方法,比如SGD。但是,SGD的收敛情况经常依赖于迭代次数,不能保证在有限次数内达到最小值。
因此,本文的目标是解决这样一个问题:在同时保证隐私和可用性的情况下,是否可以释放一个noisy “approximate” minima of the perturbed objective。
本文提出了Approximate Minima Perturbation(AMP),噪声量包含一个代表最大梯度范数容忍度的参数(maximum tolerable gradient norm)。这提供了一个梯度范数bound(也就是加入approximate minima的噪声量)和difficulty(根据norm bound来获取approximate minima的难度)之间的trade-off。如果norm bound设置为0,这个方法就会退化成标准的objective perturbation。AMP具有如下优势:
- 适用于所有的凸目标函数,之前的目标扰动只适用于目标函数是线性模型;两者都需要一些标准属性如Lipschitz continuity和smoothness。
- 第一个可行的可以利用任何现成的optimizer的满足DP的方法。
- 有competitive hyperparameter-free变体。
Related Work
放一张大佬做报告时候的截图:

DP convex ERM:
[8 K. Chaudhuri, C. Monteleoni, and A. D. Sarwate, “Differentially private empirical risk minimization,” JMLR, 2011.] 提出了output和objective扰动;
[11 P. Jain and A. Thakurta, “(near) dimension independent risk bounds for differentially private learning,” in Proceedings of the 31st International Conference on International Conference on Machine Learning - Volume 32, ser. ICML’14. JMLR.org, 2014, pp. I–476–I–484.] 提出了几乎是维度独立的安全学习算法,但是只适用于标准setting。
[S. Song, K. Chaudhuri, and A. D. Sarwate, “Stochastic gradient descent with differentially private updates,” in Global Conference on Signal and Information Processing (GlobalSIP), 2013 IEEE. IEEE, 2013, pp. 245–248.]第一次提出了private SGD。
[16 R. Bassily, A. Smith, and A. Thakurta, “Private empirical risk minimization: Efficient algorithms and tight error bounds,” in Foundations of Computer Science (FOCS), 2014 IEEE 55th Annual Symposium on. IEEE, 2014, pp. 464–473] 提出了另一种private SGD,给出了optimal risk bounds。
[12 X. Wu, F. Li, A. Kumar, K. Chaudhuri, S. Jha, and J. Naughton, “Bolt-on differential privacy for scalable stochastic gradient descent-based analytics,” in Proceedings of the 2017 ACM In- ternational Conference on Management of Data, ser. SIGMOD ’17. New York, NY, USA: ACM, 2017, pp. 1307–1322.] 提出了output扰动的变体,需要使用permutation-based SGD,用这种算法的性质减少了敏感度。
[D. Kifer, A. Smith, and A. Thakurta, “Private convex empirical risk minimization and high-dimensional regression,” Journal of Machine Learning Research, vol. 1, p. 41, 2012.] [A. Smith and A. Thakurta, “Differentially private feature selec- tion via stability arguments, and the robustness of the lasso,” in COLT, 2013.] 针对高维度的稀疏回归,但是这些算法也需要获取到最小值。
Fast context-aware recommendations with factorization machines
Predicting response in mobile advertising with hierarchical importance-aware factorization machine
Approximate Minima Perturbation
可以理解为是目标扰动的一种替代方案,即使算法的输出不是扰动后的目标函数的实际最小值。本文对于目标扰动的改进:
- 目标扰动的privacy保证是在优化问题每次都可以取到精确最小值的时候成立,但是在实际的有限次迭代中,这是不可能保证的。AMP通过取近似值来解决这个问题。
- 之前的目标扰动工作[8,9]只在损失函数是GLM(Generalized Linear Model)时才成立,as they implicitly make a rank-one assumption on the Hessian of the loss $\nabla^2 l(\theta;d)$。Via a careful perturbation analysis of the Hessian, we extend the analysis to any convex loss function under standard assumptions.

AMP为目标扰动提供了一种基于收敛的方案,也就是说,一旦算法找到一个模型$\theta_{approx}$,那么被扰动的目标函数的梯度的范数$\nabla L_{priv}(\theta_{approx};D)$会在一个预先定义的阈值$\gamma$内,然后输出对$\theta_{approx}$加噪声后的$\theta_{out}$。由于扰动后的目标函数是强凸的,加入标准差为$\sigma_2$的噪声可以保证DP,$\sigma_2$线性依赖于$\gamma$。
参数$(\epsilon_1,\delta_1)$表示用于扰动目标的隐私预算,剩余的$(\epsilon_2,\delta_2)$表示被用于给近似最小值$\theta_{approx}$加噪声的隐私预算。参数$\epsilon_3$是$\epsilon_1$的一部分,用来扰动目标函数;剩下的$(\epsilon_1-\epsilon_3)$用来扰动正则项。
Experiments
实验将回答三个问题:
-
What is the cost (to accuracy) of privacy?
DP model 得到的结果和non-private的差距有多大?真实环境中cost是否足够低,以保证DP的实用性。
实验结果表明,数据集足够大的话,损失是可以忽略的。(分别在低维、高维和真实数据中做了测试。甚至在真实数据中,DP model可以达到比non-private的更好的准确率)
-
Which algorithm provides the best accuracy in practice?
所有的算法性能的顺序是否一致,针对不同的数据集是否会有所差别?
基本上本文提出的AMP都效果更好一些。某些特定条件下,private Frank-Wolfe算法更好。
-
Can Approximate Minima Perturbation be deployed without hyperparameter tuning?
是否可以不受超参数的影响?
A. Experiment Setup
分别对比四种方法中的算法:目标扰动、输出扰动、private梯度下降和private Frank-Wolfe算法。
对于目标扰动,实现了AMP算法,分别对比评估通过grid search调整超参的方案和不受超参影响的AMP变体;
对于输出扰动,实现了Private Permutation-based SGD(PSGD,文章里似乎写错了,写的Perturbation-based)算法[12],对比了凸和强凸两种变体,都是mini-batch形式的。对凸的,评估了三种不同的学习率(常数、下降的、平方根的),本文实验表明常数学习率是效果最好的;
对于private梯度下降,实现了private SGD[16]的变体,利用了[15]提出的Moments Accountant,加入了batch处理,并根据所需的迭代次数(与[16]中的固定$n^2$次迭代相比)设置了噪声参数。
对于private Frank-Wolfe,实现了[17 K. Talwar, A. Thakurta, and L. Zhang, “Private empirical risk minimization beyond the worst case: The effect of the constraint set geometry,” CoRR, vol. abs/1411.5417, 2014.]中的算法,根据[26 M. Jaggi, “Revisiting frank-wolfe: projection-free sparse convex optimization,” in Proceedings of the 30th International Confer- ence on International Conference on Machine Learning-Volume 28. JMLR. org, 2013, pp. I–427]的建议,采用减小的学习率来取得更好的准确率。和其他算法不同,这种算法拥有几乎和维度无关的error bounds,因此应该在高维数据中有更好的效果。
Datasets
低维数据表示数据个数远大于数据维度,高维数据则表示数据个数小于等于数据维度。随机shuffle数据,训练集和测试集8比2.
Sample clipping
评估的每种算法的损失函数都需要有一个Lipschitz常数。可以通过对每个样本进行bound the norm操作来实现这个需求。
对于除了private Frank-Wolfe之外的算法,为了使损失函数有$L_2$-Lipschitz常数L,可以把样本$(x_i,y_i)$的特征向量$x_i$ 裁剪为$(x_i\cdot \min(1,\frac{L}{\Vert x_i\Vert}))$。
而对private Frank-Wolfe算法,需要损失函数有a relaxed $L_1$-Lipschitz常数L,可以通过bound $L_{\infin}$-norm of each sample $(x_i,y_i)$ by L来实现[41 定理1]。具体地,通过clip每个维度$x_{i,j}$为$\min(x_{i,j}, L)$,其中$j\in [d]$。
Hyperparameters
为了保证端到端的DP,对超参的调整也应该保证private的方式进行。[8,14,15]提出了一些方法,但是对于不同的算法不太好比较。因此本文用grid search的办法来找到每个超参的最优值。所谓格搜索,就是按照表2来考察哪个超参效果更好。
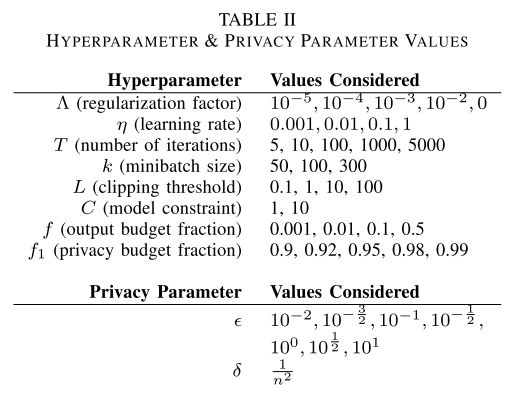
参数C是用来控制$L_1/L_2$-ball的尺寸的,这个球的作用是参数空间(要看下代码里怎么体现的)?
The parameter C controls the size of the L1/L2-ball from which models are selected by private Frank-Wolfe/the other algorithms respectively.
Algorithm Implementations
见论文中附录C和仓库“Differentially Private Convex Optimization Benchmark,” 2017. [Online]. Available: dpml-benchmark.
Experiment procedure
实验的目标是要找到准确率最高的privacy parameters。每组超参组合10次,准确率取平均值。
Non-private baseline
用Scikit-learn的LogisticRegression来训练的non-private算法,训练集和测试集都和private算法一样,训练模型时候没有进行sample clipping。
Strategy for Hyperparameter-free Approximate Minima Perturbation
设置L=1可以得到为目标函数添加噪声和对sample clipping后的信息损失之间一个比较好的trade-off。
B. Loss functions
选用logistic regression和Huber SVM。LR是带L2正则项的损失函数。
\(l(\theta,(x,y)) = \ln(1+\exp(y \langle\theta, x\rangle))+\frac{\Lambda}{2}\Vert\theta^{2}\Vert\),
其中$y\in {-1,1}$.
考虑了不带正则项的,$\Vert x\Vert\leq L$时,$L_2$-Lipschitz常数是$L$。
带正则项的,$\Vert x\Vert\leq L, \Vert\theta\Vert\leq C$,$L_2$-Lipschitz常数是$L+\Lambda C$,同时也是$(L^2+\Lambda)$-smooth的,$\Lambda$-strongly convex。
C. Experiment 1: Low-dimensional Datasets
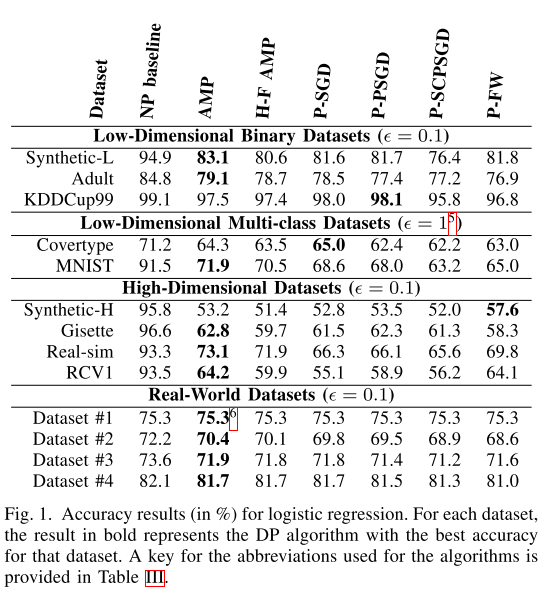
对低维数据来说,二分类的准确率显然优于多分类的准确率,因为$\epsilon$和$\delta$需要为每个类别建立的二分类器进行划分。
D. Experiment 2: High-dimensional Datasets
对高维数据来说,大部分数据上AMP算法最好,但是在Synthetic-H上,private Frank-Wolfe算法效果最好。从[11,17]中可以看到,当损失为GLM时,目标扰动和private Frank-Wolfe都有几乎和维度无关的utility guarantees。
private FW算法在模型稀疏时是最优的,而数据集Synthetic-H可以通过10个重要的特征来很好的表达出来。pFW算法每次迭代中最多增加一个特征,噪声随着迭代次数增加,但是并不随着特征总数增加,因为它随着samples的$l_{\infin}$-norm的bound增加。而AMP的noise是随着$l_2$-norm的bound增加。
E. Experiment 3: Real-world Use Cases
用了Uber的真实数据。所有结果都和non-private的baseline很接近,说明在实际中,privacy带来的损失是可以忽略的。数据集#1中,AMP效果甚至优于baseline,[18,19]已经理论论证过DP可以有正则化的作用。
[14 K. Chaudhuri and S. Vinterbo, “A stability-based validation procedure for differentially private machine learning,” in Proceed- ings of the 26th International Conference on Neural Information Processing Systems - Volume 2, ser. NIPS’13. USA: Curran Associates Inc., 2013, pp. 2652–2660.]
[15 M. Abadi, A. Chu, I. Goodfellow, H. B. McMahan, I. Mironov, K. Talwar, and L. Zhang, “Deep learning with differential pri- vacy,” in Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, ser. CCS ’16. New York, NY, USA: ACM, 2016, pp. 308–318.]
[41 R. Paulaviˇcius and J. Zilinskas,ˇ “Analysis of different norms and corresponding lipschitz constants for global optimization,” Ukio Technologinis ir Ekonominis Vystymas, vol. 12, no. 4, pp. 301– 306, 2006.]
