TCC 16
Abstract
给出了CDP的另一种形式,并基于此证明了更好的量化结果,更低的bounds,提出了一些新的问题。
Introduction
DP的一个显著缺点是,在多次计算时会degrade smoothly。比如执行k个计算任务(每个都符合$\varepsilon$-DP),然后将计算结果组合起来,会降级到$k\varepsilon$-DP。
approximate DP($(\varepsilon,\delta)$-DP),可以保证任何个体承受损失超过$\varepsilon$的概率在$\delta$以内。在$\delta$足够小的时候可以达到和pure DP差不多的隐私保护,同时permit substantially more useful analyses to be performed。
但是有时候针对一些数学分析上的抽象就不那么好用了,比如组合性的分析。“高级组合性质”指出$k$个$(\varepsilon,\delta)$-DP的任务组合起来是$(\approx \sqrt{k}\varepsilon, \approx k\delta)$-DP的。但是这个bounds应用并不广泛,因为不够紧,计算tightest的隐私保证是#P-hard的。比如对有n个元素的数据集进行k次query,每次加入高斯噪声$N(0,(\sigma/n)^2)$。则每次满足$O(\sqrt{\log(1/\delta)}/\sigma,\delta)$-DP的,根据高级组合定理,k次query后,满足$O(\sqrt{k}\log(1/\delta)/\sigma,(k+1)\delta)$-DP,但是众所周知,这个bound是可以改进为$O(\sqrt{k\log(1/\delta)}/\sigma), \sigma$-DP的。
PS:高级组合特性是<Boosting and differential privacy. FOCS10’>提出的,<The composition theorem for differential privacy. ICML15’><The complexity of computing the optimal composition of differential privacy. TCC16’>进行改进的。
《Concentrated differential privacy. CoRR16’》提出的CDP,大概是说,如果一个随机机制的privacy loss有一个比较小的均值而且是subgaussian的,那么它是满足CDP的。本文引入了另一种表达叫做”zero-concentrated differential privacy (zCDP)”,利用了概率分布之间的Renyi散度作为方法来获取隐私损失是su bgaussian的需求。
Our definition uses the R´enyi divergence between probability dis- tributions as a different method of capturing the requirement that the privacy loss random variable is subgaussian.
Zero-Concentrated Differential Privacy

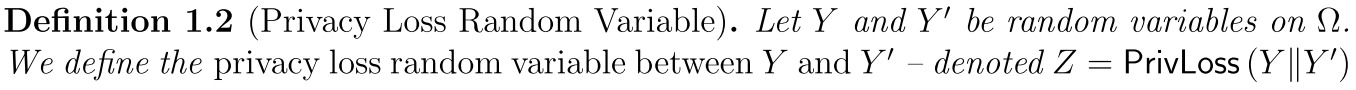
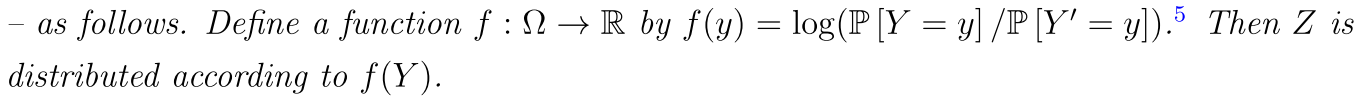
Renyi散度可以被认为是a measure of dissimilarity between distributions。privacy loss Z可以理解成是在给定输出$M(x)$或者$M(x^\prime)$时,我们可以多大程度的区分出$x$和$x^\prime$。如果$Z>0$,输出$M$更可能是来源于输入$x$的;反之,输入更可能是$x^\prime$。
一个机制$M$如果是$\varepsilon$-DP的,iff $\mathbb{P}[Z>\varepsilon]=0$;如果是$(\varepsilon,\delta)$-DP的,iff $\mathbb{P}[Z>\varepsilon]\leq \delta$。
而zCDP给出了基于privacy loss Z的矩生成函数的bound,式子2。2式还表明Z是均值较小的subgaussian的随机变量。
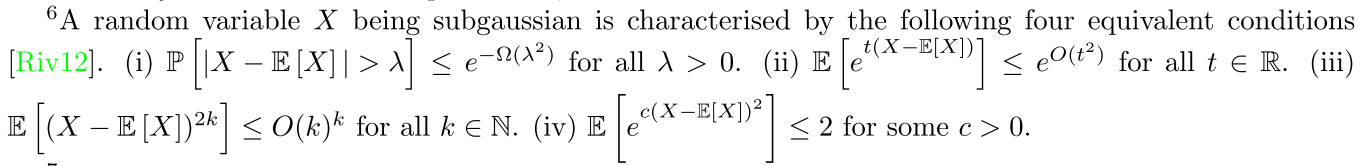
直观上,这意味着Z和均值是$\xi +\rho$,方差是$2\rho$的高斯分布类似。于是根据tail bound,有
\[\mathbb{P}[Z>\lambda+\xi+\rho]\leq e^{-\lambda^2/4\rho}\]for any $\lambda>0$。
因此zCDP需要隐私损失这一随机变量集中于0周围(这也是名字的来源)。也就是说Z大概率比较小,离0越远越不可能,也就是想要区别$x$和$x^\prime$就越难。
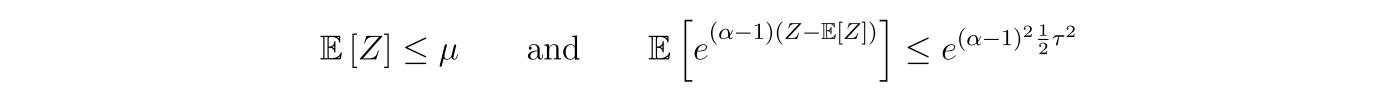
而上述CDP的定义则表明了Z需要在一个均值周围(称为mCDP(mean-CDP))。本文的定义可以看成是mCDP的一个relaxation。一个满足$(\mu,\tau)$-mCDP的机制是$(\mu-\tau^2/2,\tau^2/2)$-zCDP的。
