Infocom 2020, Zhiying Xu, Shuyu Shi, etc.
Abstract
提出一种适应性的快速的保护隐私学习算法,ADADP。该算法通过适应性的学习率提高了收敛速度从而极大的减少了privacy cost,同时通过引入适应性的噪声量,缓和了DP对模型正确率的负面影响。
Introduction
基于DP的机器学习主要有两种策略:data obfuscation和gradient obfuscation。前者的主要缺点是显著降低了模型的准确率,因为为了保证DP而加入的噪声可能太大,导致training label不可区分。后者相较于前者可能有一定的提升,但是仍有三个缺点:1)由于收敛慢导致privacy cost累积量高;2)准确率依然不够,因为加入的噪声都服从同一分布,会引起原始梯度的large distortion;3)计算低效,因为需要多次评估模型或解决每次迭代的大规模优化问题,从而使任务在计算上变得过于繁琐。
Proposed Approach
对于学习率,根据历史记录以适应性的方式对更新较为频繁的部分分配较大的学习率; 观察到训练数据中不同的维度之间的敏感度是不同的,提出对不同维度加入不同的噪声,从而实现适应性的扰动方式。
和已有的方案相比,优势是:
- privacy cost会降低,因为适应性的学习率会提高收敛速度;
- ADADP拥有可证明的隐私保证和与非隐私版本模型相当的准确率,噪声的适应依赖于different gradient components和不同的训练次数;
- computationally efficient, 因为不需要在每次迭代中解决任何额外的优化问题来决定噪声的分布。作为对比,[1]需要解决大量的非凸优化问题。
Approach
具体方法就是对学习率和噪声量进行适应性修改。
Adaptive Learning Rate
对于学习率:采用类似于RMSPROP的适应性策略。
Adaptive Noise
对于噪声量,文章首先证明(Lemma 1)对于不同维度上进行不同量的扰动(均值方差不同的高斯噪声),与所有维度都加相同分布的扰动(均值方差都相同,但是量是随机的),这二者在满足一定条件时,可以达到相同的$(\epsilon, \delta)$-DP。

举例如2维的查询函数,$s_1=12.0,s_2=6.0$。如果机制$M$满足$(\epsilon,\delta)$-DP with $\sigma_{*}=1.0$,则$M^{\prime}$也满足同样的$(\epsilon,\delta)$-DP with $\sigma_1=17.0$ and $\sigma_2=8.5$,因为$\frac{12.0^2}{17.0^2}+\frac{6.0^2}{8,5^2}\leq \frac{1}{1.0^2}$。而之前的工作会对两个维度都加上来源于同样高斯分布$N(0,13.5^2)$的噪声。
为了比较不同加噪策略的效果,利用余弦相似度比较noisy result and original result。余弦相似度越高,表明噪声对query的影响越小。假设$f^{\prime}(D)=(10.0,5.0)^T$,其余和上面例子一样。当$\sigma$不同时,余弦相似度是0.52,相同时是0.36。而当设置$\sigma_1=12.4, \sigma_2=24.8$时,余弦相似度是0.28,这正是[1]中的策略,对低敏感度的维度加入更大方差的噪声。结论是,更高敏感度的维度可以容忍更大方差的噪声。
但是应该如何计算$s_i$和$\sigma_i$呢?
将每次迭代中梯度的计算看成是一个对训练集的查询函数,$s_i$是梯度$g_t$的第$i$维的L2敏感度。对于$s_i$, 根据RMSPROP算法的思想,利用梯度的历史记录进行计算:
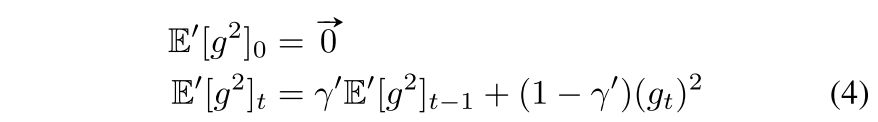
将式子4作为先验知识,$s_i$通过$\beta\sqrt{\mathbb{E^{\prime}}[g^2]_{t-1}^i}$来计算。然后进行local clipping:
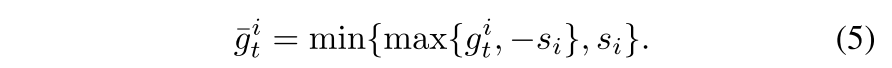
因此,$\sigma_i=\beta\sigma_{*}\sqrt{m\mathbb{E^{\prime}}[g^2]_{t-1}^i}$,m是维度。随着迭代的进行,梯度会变小,因此$\sigma_i$也会变小。表明噪声的分布不仅依赖于同一梯度的不同维度,也依赖于迭代次数。
由于最开始$\mathbb{E^{\prime}}[g^2]_{0}=0$,因此设置了参数G作为local clipping threshold,算法ADADP只在$Var[\mathbb{E^{\prime}}[g^2]] > G$时才进行local clipping。否则的话就行global clipping:
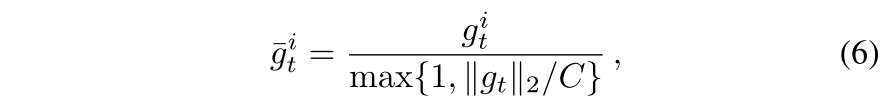
C是L2 norm clipping bound。
在Beale function上做了一个实验,比较了本文的算法,DPSGD分别和non-private算法的优化轨迹。如图1所示。
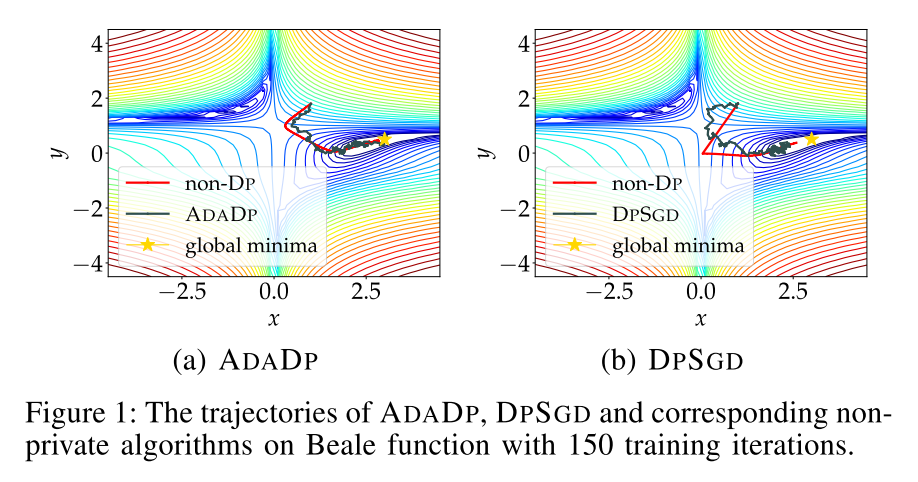
可以看出ADADP采用adaptive noise可以缓和noise对原结果的影响。
Algorithm

算法1的隐私保证由定理1给出。
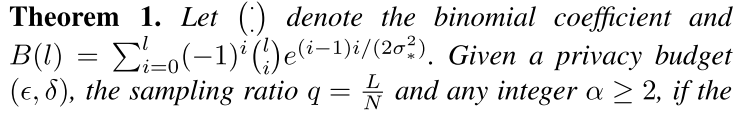

定理1覆盖了小的噪声和高采样率的领域(ccs 16中需要$\sigma \geq 1$ and $q<\frac{1}{16\sigma}$)。比如,如果用ADADP算法,设置$L=600, \sigma_*=0.9, N=60000$,定理1 bounds the privacy cost by choosing the optimal $\alpha=6$,同时模型可以在1800次迭代后达到$(4.0, 10^{-5})$-DP。
Reference
[1] L. Xiang, J. Yang, and B. Li, “Differentially-private deep learning from an optimization perspective,” in Proceedings of 38th Annual IEEE Conference on Computer Communications (INFOCOM), 2019, pp. 559–567.
