Rendle S. Factorization machines[C]//2010 IEEE International Conference on Data Mining. IEEE, 2010: 995-1000.
Abstract
FM结合了SVM和因式分解模型的优势。
可以处理实数型特征,尤其适合稀疏数据(比如推荐中很多特征经过one-hot编码后十分稀疏),而SVM却不适合。
可以在线性时间内完成。
其他类型的因式分解模型,比如SVD++, PITF or FPMC等,都是用于特定输入,需要根据不同的任务进行优化推导。
FM模型原理
对线性模型加入两两特征之间的考虑:
\[f(\mathbb{x})=w_0 +\sum_{i=1}^n w_ix_i+\sum_{i=1}^n\sum_{j=i+1}^n\langle\mathbb{v}_i,\mathbb{v_j}\rangle x_ix_j \tag{1}\]需要估计的参数有$w_0\in R,w\in R^n,\mathrm{V}\in R^{n\times k}$。其中V是辅助向量,表达为大小为k的两个向量的点乘。k是超参数。
\[\langle\mathbb{v}_i,\mathbb{v_j}\rangle = \sum_{f=1}^k v_{i,f}\cdot v_{j,f}\]对于任一正定矩阵W,总存在一个矩阵V,只要k足够大,就可以使得$W=V\cdot V^T$。但是在数据稀疏的情形中,没有足够的数据来训练复杂的W,因此应该选择小的k。对于k的限制可以在稀疏的条件下带来更好的泛化性能。
FM可以在稀疏条件下学习出这些interactions(V)是因为它通过因式分解打破了v之间的独立性。

举例比如用户A并没有评价电影ST,因此$w_{A,ST}=0$。但是因式分解可以估计它们之间的联系。首先,B和C都相似地评价了SW,$\langle \mathrm{v}B,\mathrm{v}{SW}\rangle$和$\langle \mathrm{v}C,\mathrm{v}{SW}\rangle$应该相似。A和C应该有不同的factor vector,因为他们对TI和SW有不同的评价。然后ST和SW应该有类似的factor vector,因为B对他们评价一样。综上,A对ST对比较应该和A对SW的评价类似—这也符合直觉。
接下来为了降低计算复杂度:
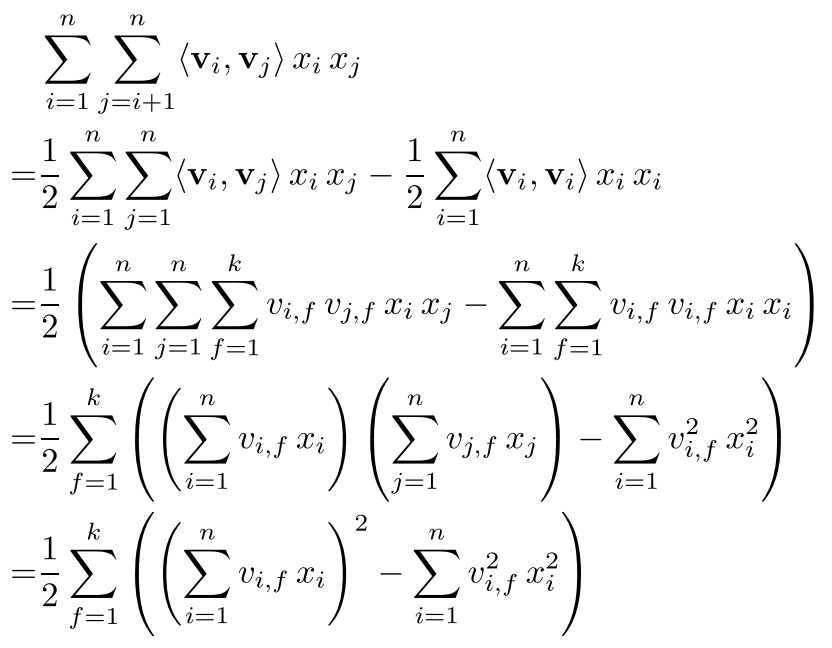
复杂度降低为线性$O(kn)$。
学习方法:
使用SGD,

总结
- FM可以在稀疏数据中学习到组合特征,甚至是那些数据中没有观测值的组合特征;
- 学习过程和参数的线性的,可以直接用SGD针对多种损失函数进行优化。
FMs vs. SVMs
SVM的多项式核:
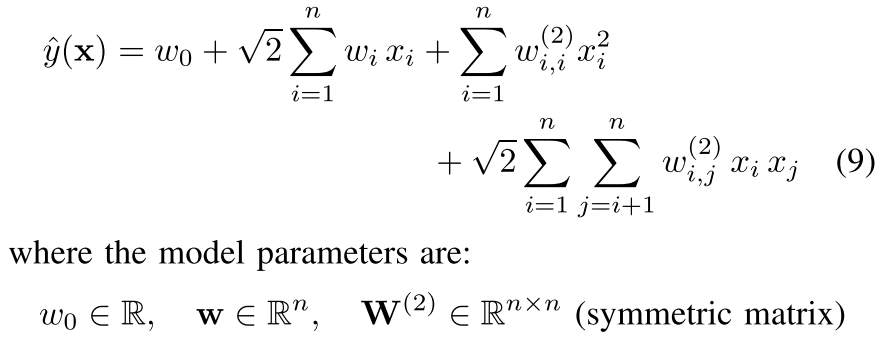
式子9和式子1的相同之处是都构造了特征之间的交叉;主要区别是SVM中每一个交叉的参数$w_{i,j}$是完全独立的,而FM中的参数是通过因式分解得到的,因此$\langle\mathrm{v}_i,\mathrm{v}_j \rangle$和$\langle\mathrm{v}_i,\mathrm{v}_l \rangle$是彼此依赖的,因为都有参数$\mathrm{v}_i$参与了计算。
线性SVM和多项式SVM对于稀疏数据为何失效:
以图1的前两栏user和item做协同过滤为例子,这里特征向量是稀疏的,只有两个元素不为0(点乘以后? 能点乘吗 列数不一样啊)。
-
线性SVM:
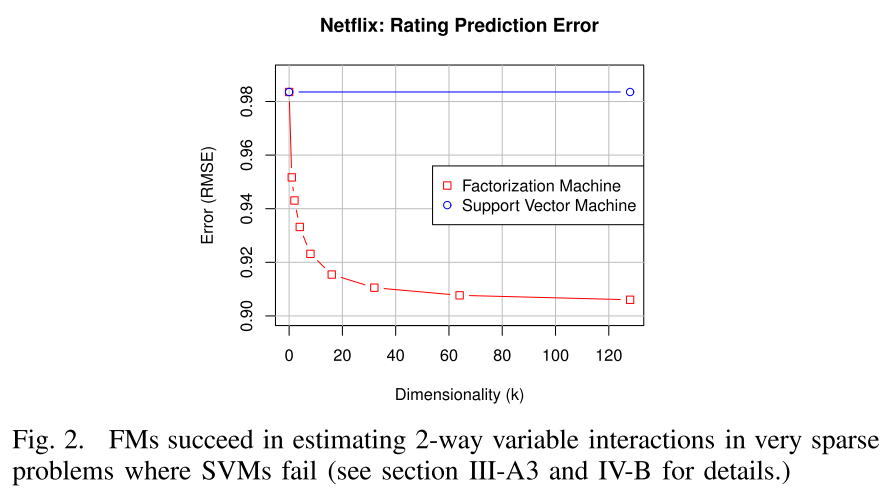
\[\hat{y}(\mathrm{x})=w_0+w_u+w_i\]由于线性模型十分简单,参数即使在稀疏情况下也可以估计,但是预测质量很低,如图2所示。
-
多项式SVM:
\[\hat{y}(\mathrm{x})=w_0+\sqrt{2}(w_u+w_i)+w_{u,u}^{(2)}+w_{i,i}^{(2)}+\sqrt{2}w_{u,i}^{(2)}\]首先$w_u$和$w_{u,u}^{(2)}$表达的是一样的,可以去掉其中之一,这样的话多项式SVM只比线性SVM多了一个交叉项$w_{u,i}^{(2)}$。典型的协同过滤问题中,对于每一个交叉参数$w_{u,i}^{(2)}$来说,只有训练数据中的观测值$(u,i)$,测试集中的$(u^\prime,i^\prime)$在训练集中是完全没有观测值的。如之前的例子,A和ST没有交互,所以此时的$w_{A,ST}^{(2)}=0$,这样多项式SVM用2次项交叉并不会对预测结果有任何帮助。
其中,$b_1,b_2 \sim N(0,\sigma)$
