Zhang J, Zhang Z, Xiao X, et al. Functional mechanism: regression analysis under differential privacy[J]. Proceedings of the VLDB Endowment, 2012, 5(11): 1364-1375.
之前的解决方案(主要是大佬的输出扰动和目标扰动)需要损失函数是强凸的等限定条件。Funtional Mechanism通过扰动目标函数的近似来满足DP。
Functional Mechanism
先介绍FM框架,然后介绍如何应用到线性回归上。
Perturbation of Objective Function
斯通-魏尔斯特拉斯定理(Stone-Weierstrass Theorem)主要是为了说明任何连续可微函数都可以用更简单的函数来一致逼近,像多项式:
\(f(t_i,w)=\sum_{j=0}^J\sum_{\phi\in\Phi_j} \lambda_{\phi t_i} \phi(w)\),
其中,$f(t_i,w)$是回归模型的损失函数,$w$是参数,$t_i = (x_i,y_i)$,$\lambda_{\phi t_i}$是多项式系数,$\phi(w)$是一个或多个$w$的乘积,比如$(w_1)^3\cdot w_2$,$\Phi$是所有可能的幂次$j$的集合。

有一个问题就是插入的噪声量过大时,目标函数可能unbounded,导致无意义的回归结果。
Application to Linear Regression
对于线性回归来说,目标函数直接展开就可以得到对应的多项式函数:
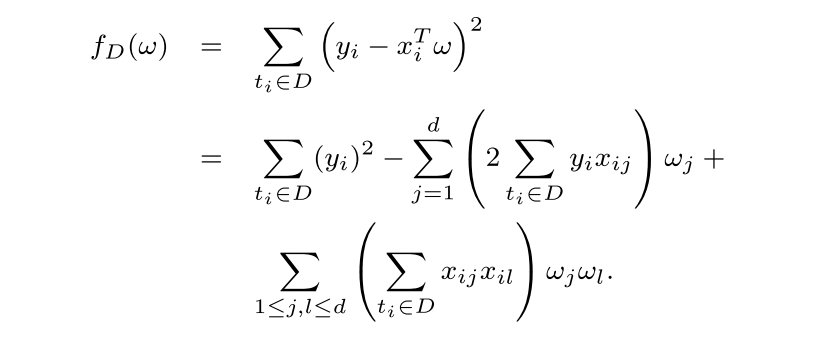
将特征都归一化以后,$|\mathbb{x}| \leq 1$,对应的
\[\Delta \leq 2 \max_{t=(x,y)}(y^2+2\sum_{j=1}^{d} yx_{(j)}+\sum_{1\leq j,l\leq d}x_{(j)}x_{(l)})\]\(\leq 2(1+2d+d^2)\).
这样的话,对每个系数加入$Lap(\frac{2(d+1)^2}{\varepsilon})$的噪声即可保证DP。
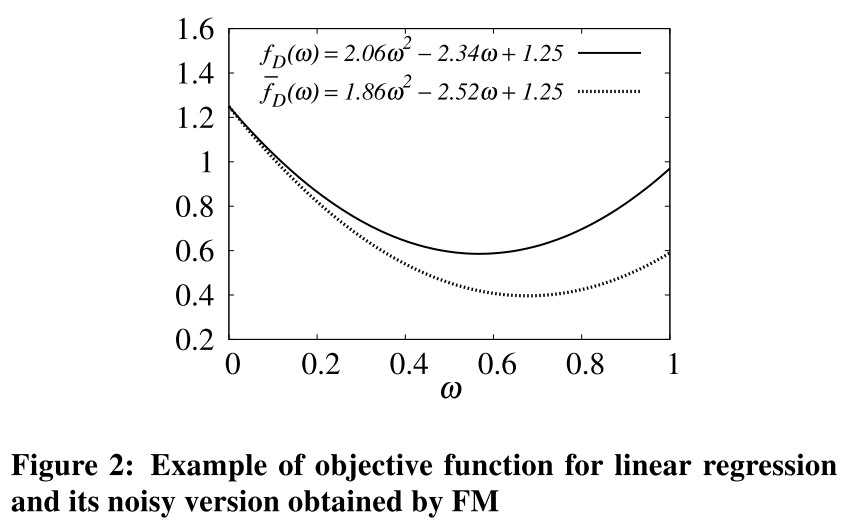
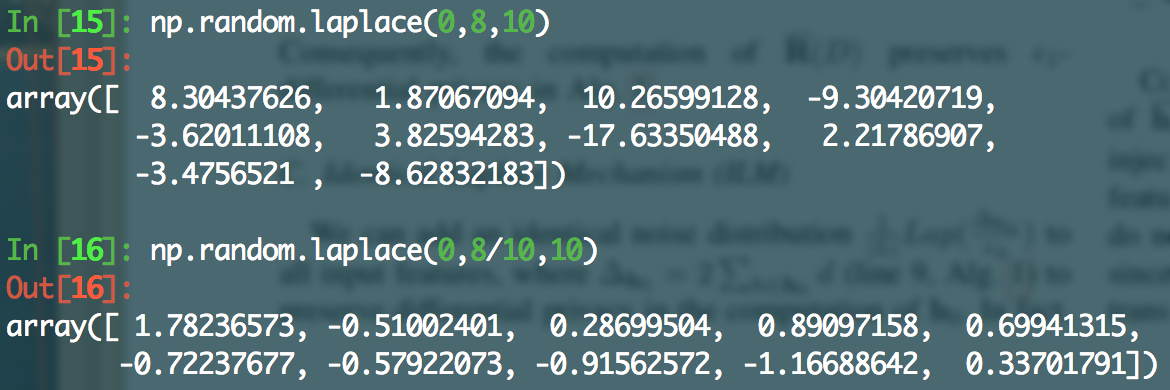
图2举了个例子,特征x是1维的,所以$\Delta=8$,然后用图2表明经过噪声混淆近似后的损失函数是相近的。(但是,文中并没有给出$\varepsilon$是用了多大的,8其实是一个挺大的量了,如果维度增加,那噪声量大的一批,还能近似回归了嘛?附图给出两组各10个laplace噪声在$\varepsilon=1,10$时候的噪声大小)
Polynomial Approximation of Objective Functions
像算法1这类工作,一个很关键的点是目标函数的多项式形式只包含terms with bounded degrees。但是这个条件不是所有的回归都满足,比如上述线性回归满足,而logistic回归则不满足。因此,这部分将基于泰勒展开对目标函数进行多项式近似。
Expansion
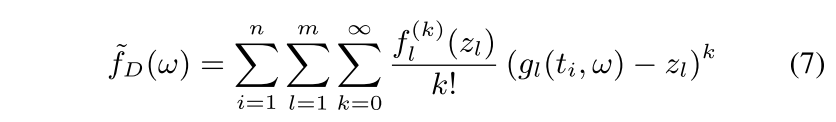
对于logistic回归来说,损失函数
\(f(t_i,w) = \log(1+\exp(x_i^T w))-y_ix_i^Tw\),
那么令$g_1(t_i,w)=x_i^Tw, g_2(t_i,w)=y_i x_i^Tw, f_1(z)=\log(1+\exp(z)),f_2(z)=z$,则
\(f(t_i,w) = f_1(g_1(t_i,w))-f_2(g_2(t_i,w))\).
对于$f_2$来说,$f_2^{(k)}=0, k>1$,对于式子7,令$z_l=0$,则有
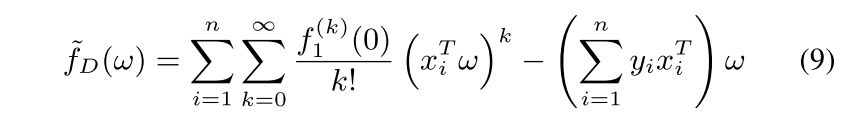
此时仍有两个问题需要解决,一是有一个无穷项,二是$f_{1}^{(k)}(0)$没有闭式解。
Approximation
为此,截断了泰勒展开,去掉大于2的阶。(上面这都可以洋洋洒洒加出来半页内容。。。。)

然后给出了10和7差的上界和下界。结论是它们的差距(average error)不超过0.015.
Application to Logistic Regression

将泰勒展开后的损失函数传给算法1,得到保护隐私的模型参数。
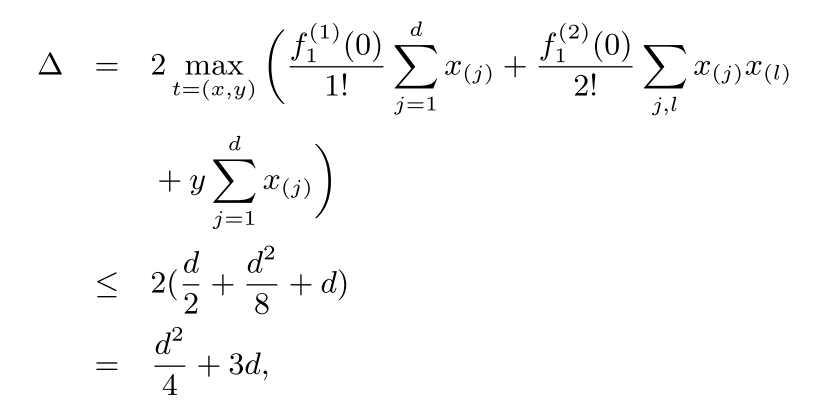
(这在d变大时候也够喝一壶的啊)
Avoiding Unbounded Noisy Objective Functions
如图2的例子,如果二次项系数加噪声后变为负的,就没有了最小的解。一种简单的解决办法是一旦出现这种unbounded的情况,就重跑FM算法直到可以求出最优解。这种算法会把隐私预算翻倍,满足$2\varepsilon$-DP。
另外两种方法是正则化和Spectral Trimming。
Regualrization
FM将目标函数转化成了二次多项式$\hat{f}_D(w)$,然后在系数上加入扰动以保证隐私。令
\[\hat{f}_D(w)=w^TMw+\alpha w+\beta \tag{1}\]代表上述二次多项式的矩阵表达(matrix representation)。
\[\bar{f}_{D}(w)=w^{T}(M^{\*})w+\alpha^{\*}w+\beta^{\*} \tag{2}\](2)式表示其加入Laplace噪声的版本。(线性代数告诉我们,)M必须是对称而且正定的[3]。为了保证加入噪声后$f$仍然是bounded的,就需要保证$M^*$也是对称而且正定的。
$M^*$的对称性可以通过如下两步来保证:
i) 加入噪声矩阵的上半三角部分;
ii) 将上半三角的元素拷贝到对应的下半三角。
由于没有现成的把一个正定矩阵以满足DP的形式转化成另一个矩阵的方法,本文采用了一种启发式的方法regularization来源于regression分析的文章[4,5]。本文对$M^*$主对角线的每个元素都加了一个正数$\lambda$,于是(2)变成了(3)的样子。
尽管正则化通常用在regression中避免过拟合,它也可以用来得到一个bounded $\bar{f}_D(w)$。如图2所示,用二维数据库为例,d=1,此时只要$M^*+\lambda{I}$是正的,就可以得到最小值。因此,只要$\lambda$足够大,就可以保证bounded。
对于$d\ge1$的情况,合理的large $\lambda$意味着$M^*+\lambda{I}$的特征值都是正的,$M^*+\lambda{I}$也就是正定的。
Meanwhile, as long as $\lambda$ does not overwhelm the signal in $M^\∗$, it would not significantly degrade the quality of the solution to the regression problem.
本文的实验中,我们观察到加入M中Laplace噪声标准差的4倍是一个比较好的$\lambda$取值。而这样设置$\lambda$不会造成隐私保证的降低,因为噪声的标准差不会泄漏任何有关数据集的信息。
但是仍然有一定几率无法得到最小值,即使是正则化以后,于是有了下面这种办法。
Spectral Trimming
\[\bar{f}_{D}(w)=w^{T}(M^{\*}+\lambda{I})w+\alpha^{\*}w+\beta^{\*} \tag{3}\]是带正则项的noisy目标函数。 $\bar{f}_D(w)$是unbounded的,当且仅当$M^{*}+\lambda I$不是正定时成立(当且仅当至少有一个特征值是非正的),也就是说,要避免非正特征值的出现。所以,直接去掉非正特征值即可。(直观上,非正元素都是由于噪声引起的,所以不会引起明显的useful information损失。去掉它们不会破坏$\epsilon$-DP,由于删除是基于矩阵$M^*$的,而不是输入数据集。
Experiments
实验对比了DPME[1], Filter-Priority (FP)[2], NoPrivacy, 和Truncated。
DPME is the state-of-the-art method for regression analysis under $\varepsilon$-differential privacy, while FP is an $\varepsilon$-differentially private technique for generating synthetic data that can also be used for regression tasks. Truncated returns the parameters obtained from an approximate objective function with truncated polynomial terms.We use two datasets from the Integrated Public Use Microdata Series, US and Brazil, which contain 370, 000 and 190, 000 census records collected in the US and Brazil, respectively.
数据有14个维度,做了5折交叉验证50次,取平均结果。
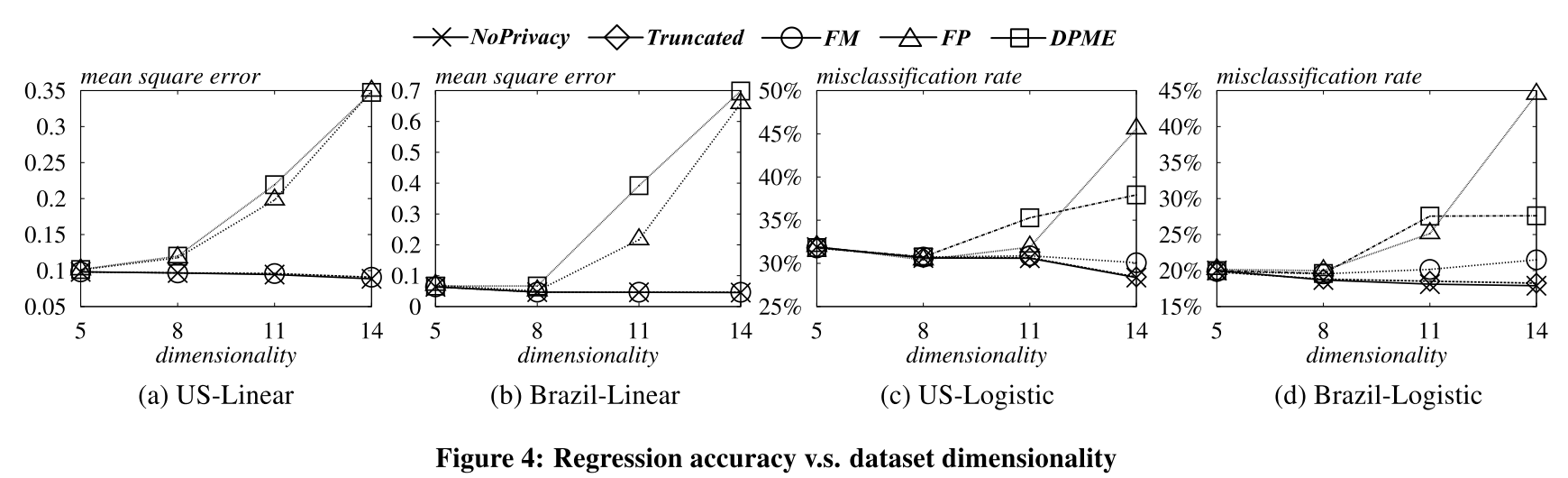
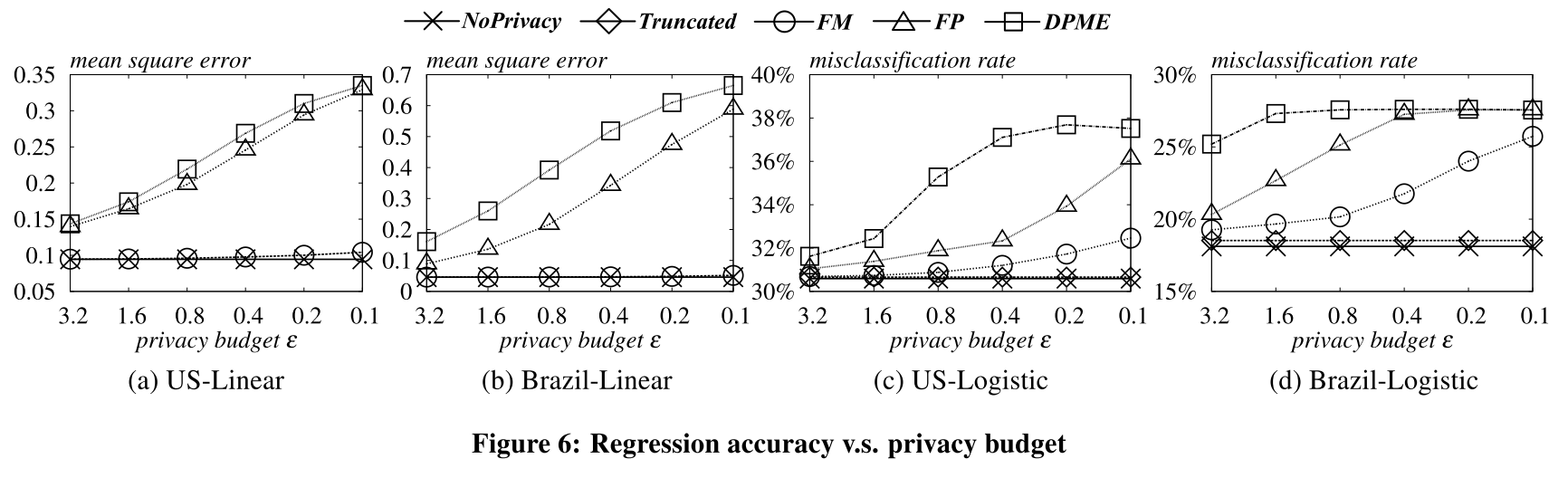
Conclusion
(效果真的能这么好吗,他这里的这个维度d实际就是数据的属性,不应该是one-hot编码后的实际维度吗?没有代码可参考就是耍流氓!)
1030更新:
找到了代码!
果然看了代码才明白的更快,以前一直理解的是,对损失函数进行二阶泰勒展开,然后对w前的系数进行扰动。还纳闷儿这么扰动结果能好吗。论文中的解决方案是第6部分。在此更新一下。
Reference
[1] J. Lei. Differentially private m-estimators. In Proceedings of the 23rd Annual Conference on Neural Information Processing Systems, 2011.
[2] G. Cormode, C. M. Procopiuc, D. Srivastava, and T. T. L. Tran. Differentially private publication of sparse data. In Proceedings ofthe 15th International Conference on Database Theory, 2012.
[3] G. Strang. Introduction to Linear Algebra. Addison Wesley, 4th edition, 1999.
[4] A. E. Hoerl and R. W. Kennard. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics, 42(1):80–86, 1970.
[5] R. Tibshirani. Regression shrinkage and selection via the lasso. Journal ofthe Royal Statistical Society, 58(1):267–288, 1996.
