Phan N H, Wu X, Hu H, et al. Adaptive laplace mechanism: Differential privacy preservation in deep learning[C]//2017 IEEE International Conference on Data Mining (ICDM). IEEE, 2017: 385-394.
提出一种PPDL的机制,可以满足:1)隐私预算的消耗不依赖于训练步骤的次数;2)根据每个输出的贡献适应性的在特征中加入噪声;3)可以应用到不同的深度神经网络中。
先直接看重点,看他是怎么做到隐私预算不依赖于迭代次数的。

算法主要分为5个步骤:
- 1~7行,通过LRP算法,获取所有第j个输入特征的平均相关性$R_j(D)$;然后加入Laplace噪声得到DP版本的;消耗隐私预算$\varepsilon_1$;
- 8~14行,在仿射变换层加入噪声,根据$\bar{R}_j$, 对噪声进行调节,对模型输出影响较小的特征,加入更多的噪声;消耗隐私预算$\varepsilon_2$;
- 15行,在DP隐层上构建其他隐藏层,形成deep private neural network;
- 16~19行,保护输出层标签$y_i$。将损失函数的参数通过插入Laplace噪声近似,消耗隐私预算$\varepsilon_3$;
- 20~30行,用SGD进行求解。
至此,每一个计算任务中需要读取原始数据集D的部分都得到了隐私保护。噪声只在预处理阶段计算相关性、第一层、和损失函数加一次,后续训练过程中不再消耗隐私预算,因此,不依赖于训练轮数。
Perturbation of the Loss Function
首先,基于泰勒展开,对损失函数取多项式近似;然后在系数上加入Laplace噪声。

用functional mechanism来对系数进行扰动,系数实际上是关于$y_{il}$的函数。

对每个系数$\phi_{l\mathbb{x}_i}^{(R)}$插入噪声$\frac{1}{\vert L\vert}Lap(\frac{\Delta_F}{\varepsilon_3})$,则满足$\varepsilon_3$-DP。
Experiments
pSGD:CCS16那篇的方法;
AdLM(Adaptive Laplace Mechanism-based CNN with ReLUs):$\varepsilon_1=\varepsilon_2=\varepsilon_3=\varepsilon/3$;
ILM(Identical Laplace Mechanism-based CNN with ReLUs):每个feature加入同样的Laplac噪声$\frac{1}{\vert L\vert}Lap(\frac{\Delta_{h_0}}{\varepsilon_2})$保证第0层的仿射变换是满足$\varepsilon_2$-DP的,$\varepsilon_2=\varepsilon_3=\varepsilon/2$.
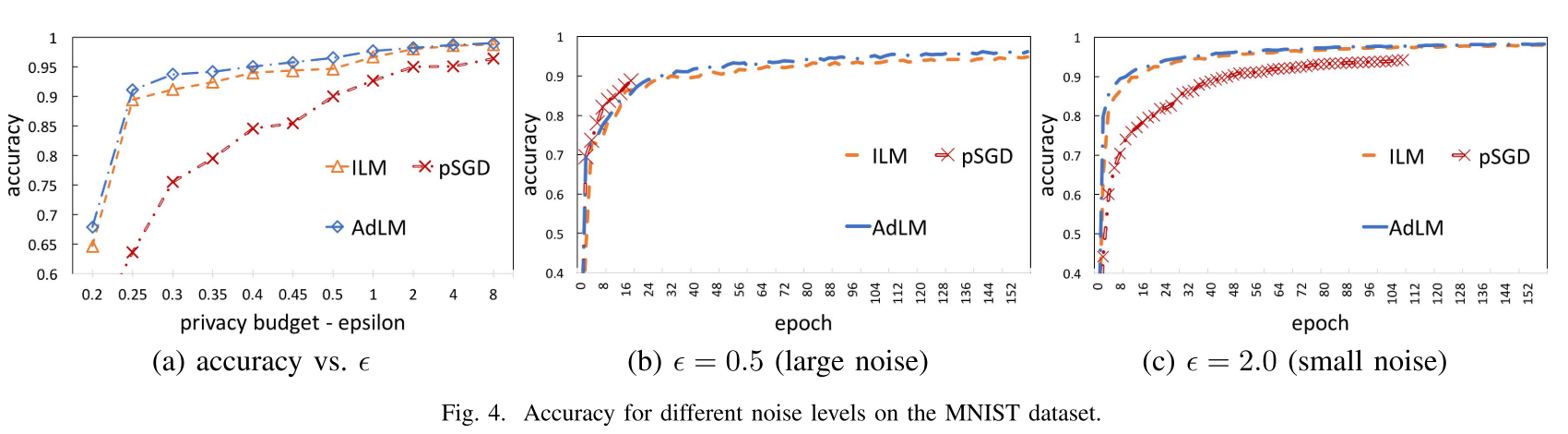
图4(a)表明AdLM和ILM都比pSGD强。图4(b)(c)表明pSGD可以较快的达到不错的准确率,但是pSGD can only be applied to train the model by using a limited number of epochs,特别是由于每步训练对隐私预算的累积。
Conclusion
(看起来挺有道理的样子,有需要的时候撸一下证明)
