Jayaraman B, Evans D. Evaluating Differentially Private Machine Learning in Practice[C]//28th USENIX Security Symposium (USENIX Security 19). Santa Clara, CA: USENIX Association. 2019.
Abstract
在实现PPML时,为了提高模型的可用性,常会选择较大的$\varepsilon$,而对这些选择对有意义的隐私所产生的影响知之甚少;此外,在使用迭代学习方法的场景中,差分隐私的变种可以提供更严密的分析,被用于降低所需的隐私预算,但隐私性和实用性之间存在难以理解的权衡。所以本文量化了这些影响。
本文发现“可以保证的隐私损失的上界(即使是高级机制)”和“可以被inference attack衡量的有效的隐私损失”存在一个巨大的鸿沟。现有的DPML方法很少为复杂的学习任务提供可接受的utility-privacy trade-offs。
Introduction
[1] 中的$\varepsilon$达到了百万级,对于隐私保护毫无意义。
对于给定的隐私预算,提高utility的一种途径是tighten the composition of DP。[2,3,4]通过提供tighter analysis of the privacy budget under composition,在添加同样噪声量的情况下,可以达到更好的privacy(更小的$\varepsilon$),因此可以在给定$\varepsilon$的情况下获得更好的utility。但是在adversarial场景下,泄漏了多少privacy呢?因此本文评估了不同DP变体不同隐私预算下的隐私泄露情况,包括在membership inference attacks下会有多少条个体训练数据被泄露。
Related work
[5,6]对现有的DP实现进行了correctness的评估。[7]提供了effectiveness of DP against attacks,但是没有明确回答$\varepsilon$应该用多少,也没有提供privacy leakage的评估。[8]考虑了放松DP notion的方式来取得更好的utility,但是也没有评估leakage。[9]是最接近本文的,评估了DP implementations against membership inference attacks,但是也没有评估不同DP变体的privacy leakage。[10]reported on extensive hypothesis testing differentially private machine learning using the Neyman-Pearson criterion, 给出了基于敌手先验知识的privacy budget设置的指导。
DP for Machine Learning
Variants of DP
[11]指出通过轻微的增加失败概率$\delta$,线性组合的$\varepsilon$的bound可以减小。
In essence, this relaxation considers the linear composition of expected privacy loss of mechanisms which can be converted to a cumulative privacy budget $\varepsilon$ with high probability bound.
Dwork把这个定义为advanced composition theorem,并且证明它可以用于任何DP机制。
另外三种常用的DP变体包括提供改进组合性质的Concentrated DP[12], Zero Concentrated DP[2], Renyi DP[4]。

虽然三种变体都利用了“the privacy loss random variable is strictly centered around an expected privacy loss”这一事实来获取tighter analysis of cumulative privacy loss,对于给定的隐私预算可以减少所需要的噪声量,从而提高utility。但是噪声减少给privacy leakage带来了什么样的实际影响呢?
变体是用了不同的技术来分析机制的组合性,也就是说它们本身是不影响添加的噪声量的。它们做的是enable a tighter analysis of the guaranteed privacy。这意味着对于固定的隐私预算,放松了的定义可以通过添加比looser analyses所需要更少的噪声来满足,因此 result in less privacy for the same $\varepsilon$ level。
[12]指出DP机制的privacy loss服从sub-Gaussian分布。也就是说,privacy loss被严格分布在privacy loss的期望(均值)周围,the spread通过sub-Gaussian分布的方差来控制。多个DP机制的组合可以通过组合单个sub-Gaussian分布的均值和方差来实现。这可以被转化为类似于advanced composition theorem的privacy budget累积,从而减少每个机制需要的噪声量。这就是CDP:
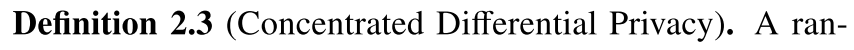



Moments Accountant. MA追踪组合过程中privacy loss的矩的bound,可以看作是RDP的一个实例。
DP Methods for ML

三种典型的privacy机制,本文关注gradient perturbation,每次迭代需要noise in the scale of $\frac{2}{n\varepsilon}$。
深度学习中目标函数是非凸的,因此不能直接用output and objective perturbation。这时可以用凸的多项函数来代替非凸函数[13,14],然后采用objective perturbation。另一种更简单的方法是直接用梯度扰动的方案,此时需要对梯度进行适当的clip,以得到sensitivity bound。
Implementing DP
Binary classification.
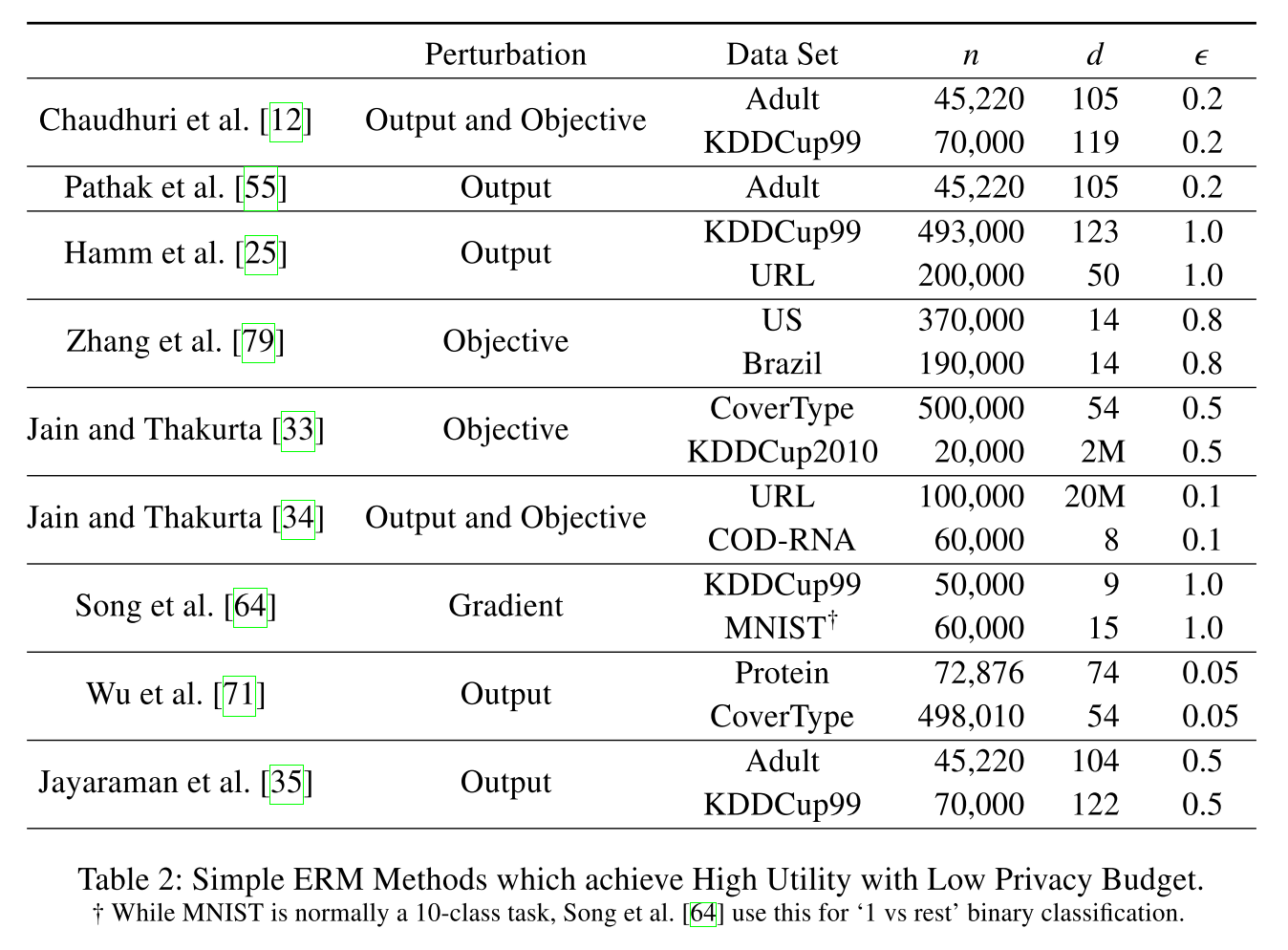
[15,CM09]首次给出了private logistic regression的实现,输出扰动和目标扰动两种方式,[16,CMS11(12)]扩展到了更通用的ERM算法上。但是需要强凸、目标函数光滑、数据低维,简单的二分类任务。
后来提出的方法,包括针对高维数据[17(JT13), 18(JT14), 19],不需要强凸假设的[20],relax the assumptions on data and objective functions[21,22,23]。这些都是理论的,除了[17,18]给出了实现。
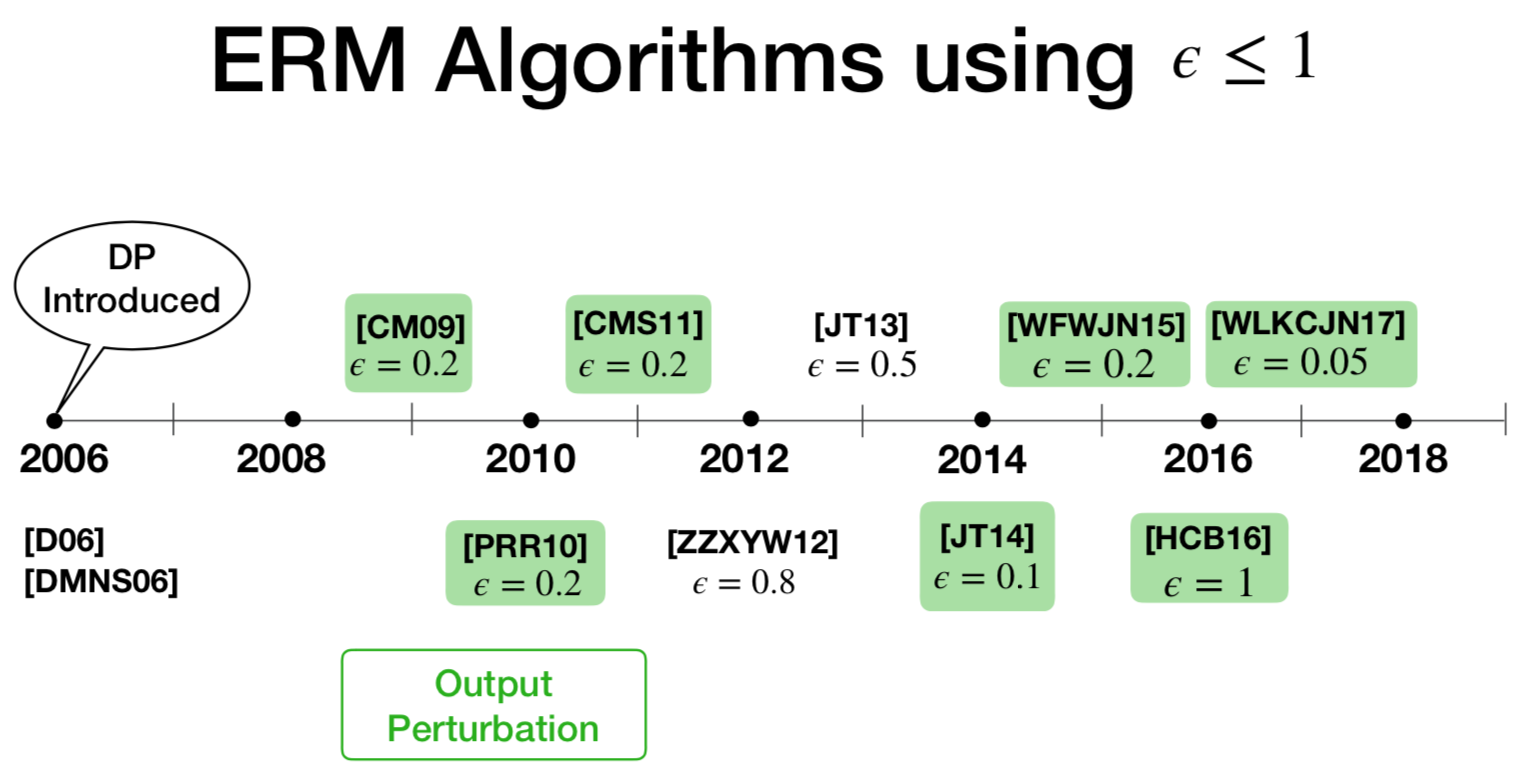
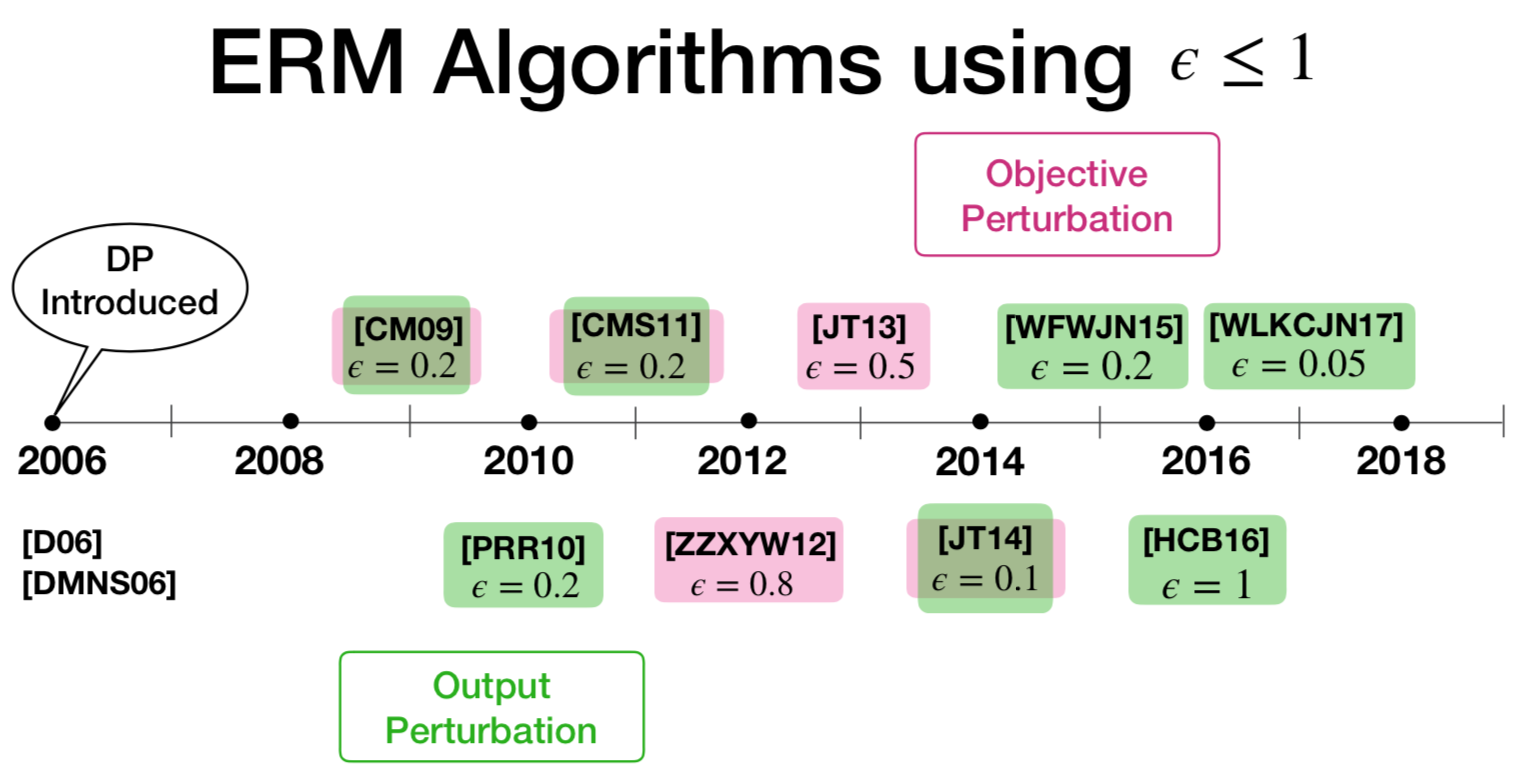
Complex learning tasks.

直接应用二分类的那些方法到更复杂的学习任务中,需要更高的隐私预算。比如,ERM的online版本[24(32)]需要$\varepsilon$到10才能得到可接受的utility。[13(56),14(57)]通过把深度学习中的非线性函数替代成多项式近似的,然后应用目标扰动的方式,在$\varepsilon=1$的情况下,得到了不错的utility。但是,这种方法并不是针对深度学习的通用方法,会限制模型的学习能力。表3是复杂任务的隐私学习算法对比。
Machine learning with other DP definitions.
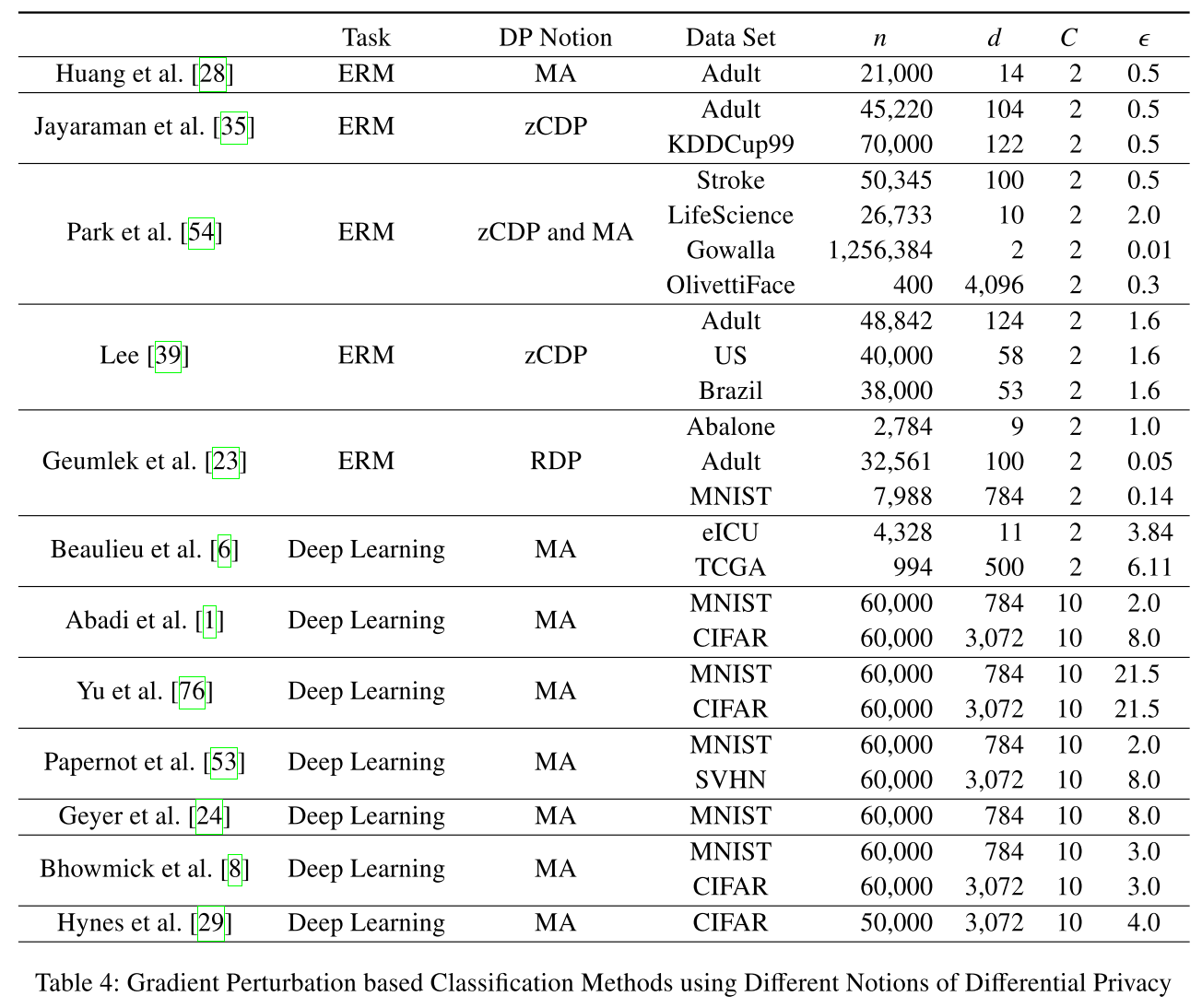
[28] Zonghao Huang, Rui Hu, Yanmin Gong, and Eric ChanTin. DP-ADMM: ADMM-based distributed learning with DP
[35] Bargav Jayaraman, Lingxiao Wang, David Evans, and Quanquan Gu. Distributed learning without distress: Privacy-preserving Empirical Risk Minimization. In Advances in Neural Information Processing Systems, 2018.
[54] Mijung Park, Jimmy Foulds, Kamalika Chaudhuri, and MaxWelling. DP-EM: Differentially private expectation maximization. In Artificial Intelligence and Statistics, 2017.
[39] Jaewoo Lee. Differentially private variance reduced stochastic gradient descent. In International Conference on New Trends in Computing Sciences, 2017.
[23] Joseph Geumlek, Shuang Song, and Kamalika Chaudhuri. Rényi differential privacy mechanisms for posterior sampling. In Advances in Neural Information Processing Systems, 2017.
[6] Brett K Beaulieu-Jones, William Yuan, Samuel G Finlayson, and Zhiwei Steven Wu. Privacy-pre- serving distributed deep learning for clinical data. arXiv:1812.01484, 2018.
[1] Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan McMahan, Ilya Mironov, Kunal Talwar, and Li Zhang. Deep learning with differential privacy. In ACM Conference on Computer and Communications Security, 2016.
[76] Lei Yu, Ling Liu, Calton Pu, Mehmet Emre Gursoy, and Stacey Truex. Differentially private model publishing for deep learning. In IEEE Symposium on Security and Privacy, 2019.
[53] Nicolas Papernot, Martín Abadi, Úlfar Erlingsson, Ian Goodfellow, and Kunal Talwar. Semi-supervised knowledge transfer for deep learning from private training data. In International Conference on Learning Representations, 2017.
[24] Robin C Geyer, Tassilo Klein, and Moin Nabi. Differen- tially private federated learning: A client level perspec- tive. arXiv:1712.07557, 2017.
[8] Abhishek Bhowmick, John Duchi, Julien Freudiger, Gaurav Kapoor, and Ryan Rogers. Protection against reconstruction and its applications in private federated learning. arXiv:1812.00984, 2018.
[29] Nick Hynes, Raymond Cheng, and Dawn Song. Efficient deep learning on multi-source private data. arXiv:1807.06689, 2018.
Inference Attacks on ML
Membership Inference
目的是为了推断给定的一个记录是否在训练集中。[25]首次提出了这种攻击,黑盒模型。出发点是机器学习模型在其训练数据和初次遇见的数据上的表现往往不同,可据此推断某条数据是否在其训练数据集中。据此想训练一个attack model来对输入进行推断,给出某个输入是否存在与训练集的置信分数。但是由于不知道训练数据集,所以提出了shadow model,用来生成训练集。[26]提出了白盒模型的攻击,可以进入目标模型,且指导模型的training loss的均值,如果输入数据通过计算后,loss小于模型的loss均值,那么就认为它存在于训练集中。
Connection to DP. 直观上看,DP和membership attack是一对矛盾。membership advantage定义为敌手的true and false positive rates的区别,[26]给出了二者的联系:如果一个算法满足$\varepsilon$-DP,那么敌手的advantage is bounded by $e^{\varepsilon}-1$。
Evaluation
做实验来测量敌手可以从模型中推断出多少。membership attack得出的结论仅限于information leakage的下限。DP提供了leakage的上限。结论是implemented privacy protections do not appear to provide sufficient privacy.
Setup
不同的变体:naive composition(NC), advanced composition (AC), zero-concentrated differential privacy (zCDP) and Rényi differential privacy (RDP).
Accuracy loss:
\[Accuracy Loss=1-\frac{Accuracy\ of\ Private\ Model}{Accuracy\ of\ Non-Private\ Model}\]Privacy Leakage:
\[TPR-FPR\](本身为正,被预测为正的概率 - 本身为负,被预测为正的概率) TPR = TP /(TP + FN)FPR = FP /(FP + TN)
0表示没有leakage。(不是很理解??)

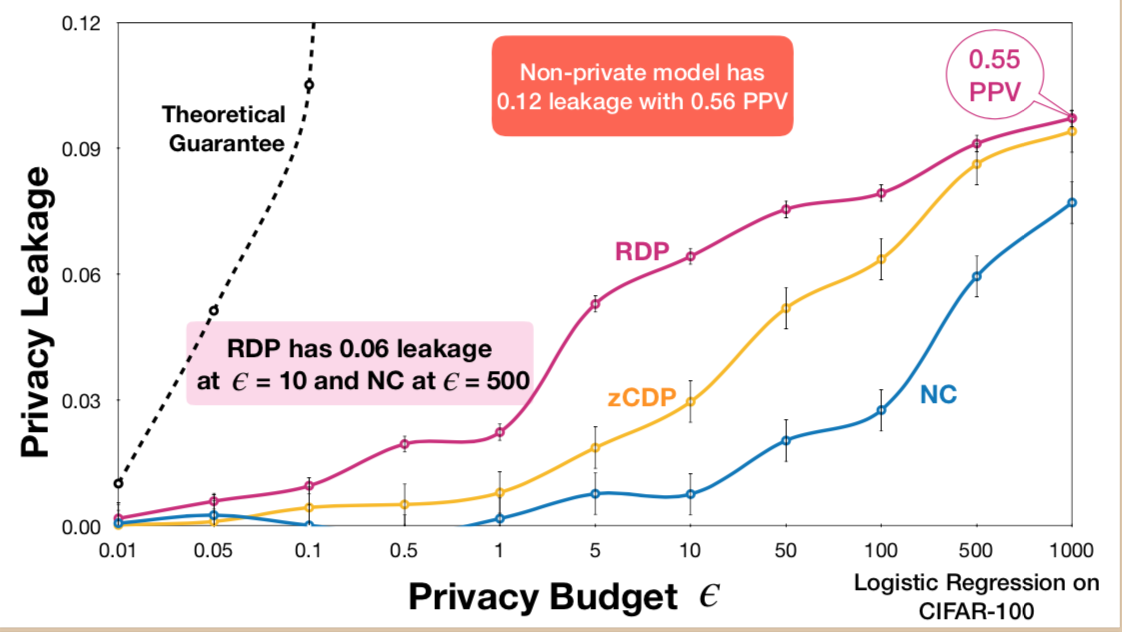
(实验待补,饿了,觅食去。)
(一年后,我来开始补实验了。。唉)

图1左和右比较,表示batch gradient clipping基本上不能看,所以后边的实验都是用的per-instance gradient clipping。
从图1右可以看出,Naive Composition在$\epsilon\leq 10$时准确率为0.01,是100个分类里的随机猜测,基本上不可用,$\epsilon=1000$时,loss几乎为0。当$\epsilon \geq 100$时,Advanced Composition加入了比NC更多的噪声,因此不应该采用。zCDP和RDP分别在$\epsilon =500$和$\epsilon=50$时,loss接近0,和NC相比是量级的减小。对于相同的privacy budget,这些DP的变体只需要更少的噪声来达到。

图2中的理论上界是$e^{\epsilon}-1$,表示$\epsilon$-DP下的privacy leakage。三个图都表明,inference attacks还有很大的提升空间。从图1(b)和图2中可以看出,RDP在$\epsilon=10$时可以取得和NC在$\epsilon=500$时类似的utility和privacy leakage。
被attack的程度只和utility相关。$\epsilon$越小,隐私保护程度越高,这个应该是只能在同一种DP机制里成立。
Conclusion
通常使用的$\varepsilon$ values的组合和各种DP的变体,并不能提供很好的utility-privacy trade-offs。What the state-of-the-art inference attacks can infer和DP可以提供的保证之间还存在巨大的差距。
直白一点就是,较好的utility下,任何DP变体提供的隐私保证基本上是无意义的,尽管通过attack观察到的泄露也是相对较低的(为什么这么说,泄露低了不就是良好的保证么??)。
Research is needed to understand the limitations of inference attacks, and eventually to develop solutions that provide desirable, and well understood, utility-privacy trade-offs.
Reference
[1] Reza Shokri and Vitaly Shmatikov. Privacy-preserving deep learning. In ACM Conference on Computer and Communications Security, 2015.
[2] Mark Bun and Thomas Steinke. Concentrated differential privacy: Simplifications, extensions, and lower bounds. In Theory ofCryptography Conference, 2016.
[3] Cynthia Dwork and Guy N. Rothblum. Concentrated differential privacy. arXiv:1603.01887, 2016.
[4] Ilya Mironov. Rényi differential privacy. In IEEE Computer Security Foundations Symposium, 2017.
[5] Zeyu Ding, Yuxin Wang, Guanhong Wang, Danfeng Zhang, and Daniel Kifer. Detecting violations of differential privacy. In ACM Conference on Computer and Communications Security, 2018.
[6] Michael Hay, Ashwin Machanavajjhala, Gerome Miklau, Yan Chen, and Dan Zhang. Principled evaluation of differentially private algorithms using DPBench. In ACM SIGMOD Conference on Management of Data, 2016.
[7] Nicholas Carlini, Chang Liu, Jernej Kos, Úlfar Erlingsson, and Dawn Song. The Secret Sharer: Evaluating and testing unintended memorization in neural networks. In USENIX Security Symposium, 2019.
[8] Ninghui Li,Wahbeh Qardaji, Dong Su,Yi Wu, andWein- ing Yang. Membership privacy: A unifying framework for privacy definitions. In ACM Conference on Computer and Communications Security, 2013.
[9] Md Atiqur Rahman, Tanzila Rahman, Robert Laganière, Noman Mohammed, and Yang Wang. Membership inference attack against differentially private deep learning model. Transactions on Data Privacy, 2018.
[10] Changchang Liu, Xi He, Thee Chanyaswad, Shiqiang Wang, and Prateek Mittal. Investigating statistical privacy frameworks from the perspective of hypothesis testing. Proceedings on Privacy Enhancing Technolo- gies, 2019.
[11] Cynthia Dwork and Aaron Roth. The Algorithmic Foundations of Differential Privacy. Foundations and Trends in Theoretical Computer Science, 2014.
[12] Cynthia Dwork and Guy N. Rothblum. Concentrated differential privacy. arXiv:1603.01887, 2016.
[13] NhatHai Phan, Yue Wang, Xintao Wu, and Dejing Dou. Differential privacy preservation for deep auto-encoders: An application of human behavior prediction. In AAAI Conference on Artificial Intelligence, 2016.
[14] NhatHai Phan, Xintao Wu, and Dejing Dou. Preserving differential privacy in convolutional deep belief net- works. Machine Learning, 2017.
[15] Kamalika Chaudhuri and Claire Monteleoni. Privacy-preserving logistic regression. In Advances in Neural Information Processing Systems, 2009.
[16] Kamalika Chaudhuri, Claire Monteleoni, and Anand D. Sarwate. Differentially private Empirical Risk Minimization. Journal ofMachine Learning Research, 2011.
[17] Prateek Jain and Abhradeep Thakurta. Differentially private learning with kernels. In International Conference on Machine Learning, 2013.
[18] Prateek Jain and Abhradeep Guha Thakurta. (Near) Dimension independent risk bounds for differentially private learning. In International Conference on Machine Learning, 2014.
[19] Kunal Talwar, Abhradeep Thakurta, and Li Zhang. Private Empirical Risk Minimization beyond the worst case: The effect of the constraint set geometry. arXiv:1411.5417, 2014.
[20] Kunal Talwar, Abhradeep Thakurta, and Li Zhang. Nearly Optimal Private LASSO. In Advances in Neural Information Processing Systems, 2015.
[21] Adam Smith and Abhradeep Thakurta. Differentially Private Feature Selection via Stability Arguments, and the Robustness of the Lasso. In Proceedings ofConfer- ence on Learning Theory, 2013.
[22] Di Wang, Minwei Ye, and Jinhui Xu. Differentially private Empirical Risk Minimization revisited: Faster and more general. In Advances in Neural Information Processing Systems, 2017.
[23] Jiaqi Zhang, Kai Zheng,Wenlong Mou, and Liwei Wang. Efficient private ERM for smooth objectives. In International Joint Conference on Artificial Intelligence, 2017.
[24] Prateek Jain, Pravesh Kothari, and Abhradeep Thakurta. Differentially private online learning. In Annual Conference on Learning Theory, 2012.
[25] Reza Shokri, Marco Stronati, Congzheng Song, and Vitaly Shmatikov. Membership inference attacks against machine learning models. In IEEE Symposium on Security and Privacy, 2017.
[26] Samuel Yeom, Irene Giacomelli, Matt Fredrikson, and Somesh Jha. Privacy risk in machine learning: Analyzing the connection to overfitting. In IEEE Computer Security Foundations Symposium, 2018
