Huang Z, Hu R, Guo Y, et al. DP-ADMM: ADMM-based distributed learning with differential privacy[J]. IEEE Transactions on Information Forensics and Security, 2019.
发表在TIFS2019上,从摘要来看,是针对分布式学习的Alternating direction method of multipliers(ADMM)优化方法提出了DP的版本。指出以前的工作在高privacy guarantee下,utility都比较低,而且还需要假设目标函数是光滑且强凸的。为此,本文提出了DP-ADMM,结合了approximate augmented Lagrangian function和随时间可变的高斯噪声,在同样隐私保证的条件下,可以得到更高的utility。同时,还采用了moments accountant方法来分析端到端的privacy loss,证明了收敛性,提供了明确的utility-privacy tradeoff。
Goals and Assumptions
本文假设损失函数$\ell(\cdot)$和正则项$R(\cdot)$都是凸的,但不一定是光滑的。采用的网络结构是星型的,(自己说可以扩展到其他拓扑,比如去掉中心节点,邻居节点连接起来,我认为是官方套话,可以学习一下)。
本文的主要目的是保证不被敌手推断出参与者的数据信息。没有假设任何可信第三方,中心aggregator可以是honest-but-curious的。
ADMM with Primal Variable Perturbation (PVP)
这种方法是[1]提出的,实际上就是output perturbation的分布式版本。[2]提出的输出扰动需要假设损失函数$\ell(\cdot)$和正则项$R(\cdot)$都是光滑的,$R(\cdot)$还得是强凸的,损失函数的导数的L2 norm要bounded by $c_1$,此时$w_i^k$的L2 sensitivity就是$2c_1/m_i(\lambda/n+\rho)$,噪声量$\sigma_i=2c_1\sqrt{2\ln(1.25/\delta)}/(m_i(\lambda/n+\rho)\varepsilon)$可以保证每次迭代满足$(\varepsilon,\delta)$-DP,其中n是agents个数,m是数据集个数,$\lambda$是正则项参数,$\rho$是惩罚参数,$\gamma_i^k$是Dual variable from agent i in k-th iteration。如算法2所示。

但是,这种方法有问题:噪声量太大会破坏收敛性,尤其是k也很大时;还需要损失函数光滑和正则项强凸。
DP-ADMM
标准的ADMM中,augmented Lagrangian function:
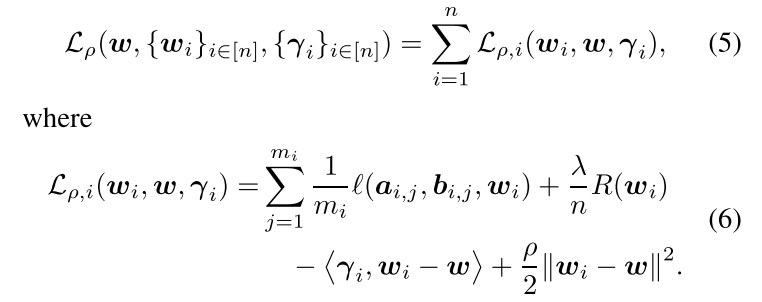
本文中,intuition是,为了保证总体的收敛,每次迭代不需要特别精确。所以,


算法3和算法2的区别在三个方面:
-
用近似的augmented Lagrangian function代替原函数
replaces the objective function with its first-order approximation at $\tilde{w}_i^{k−1}$, which is similar to the stochastic mirror descent.
-
$\frac{|w_i-\tilde{w}_i^{k-1}|}{2\eta_i^k}$保证了$w_i^k$和$w_i^{k-1}$的一致性(consistency),尤其是当k很大的时候。随着k的增加,the update model would change more smoothly。
-
$\sigma_{i,k}^2$是随着迭代次数的增加而减小的。这样做是为了减小噪声产生的影响和保证收敛性。
重点关注文章是怎么应用的moments accountant和time-varying Gaussian noise
$L_2$-norm Sensitivity
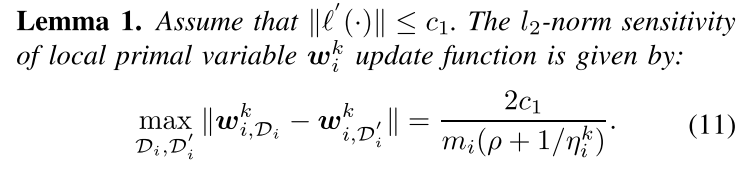
证明方法和output perturbations类似。
Time-varying Gaussian noise

Use moments accountant method to analyze the total privacy leakage

(这个看起来似乎不像是用moments accountant来确定的隐私损失啊)
Convergence Analysis
分析了非光滑凸目标函数和光滑凸目标函数情况下$\eta_i^k$的设置情况。
Performance
用UCI的Adult数据集,48842个样本。通过预处理转化为104个特征。每次模拟sample 40000个样本用来训练,5222个用来测试。训练数随机据切分成n组。设置总迭代次数$k=100$,惩罚参数$\rho=0.1$,正则参数$\lambda/n=10^{-6}$,10-cross-validation in non-private setting.
DPSGD就是CCS16 google那篇,这里设置学习率0.1,采样率1(这个有点不妥吧,采样率低了迭代次数才能上去,才能准确吧。。)
然后比较了不同参数下的收敛、准确率和计算开销,10次求平均。
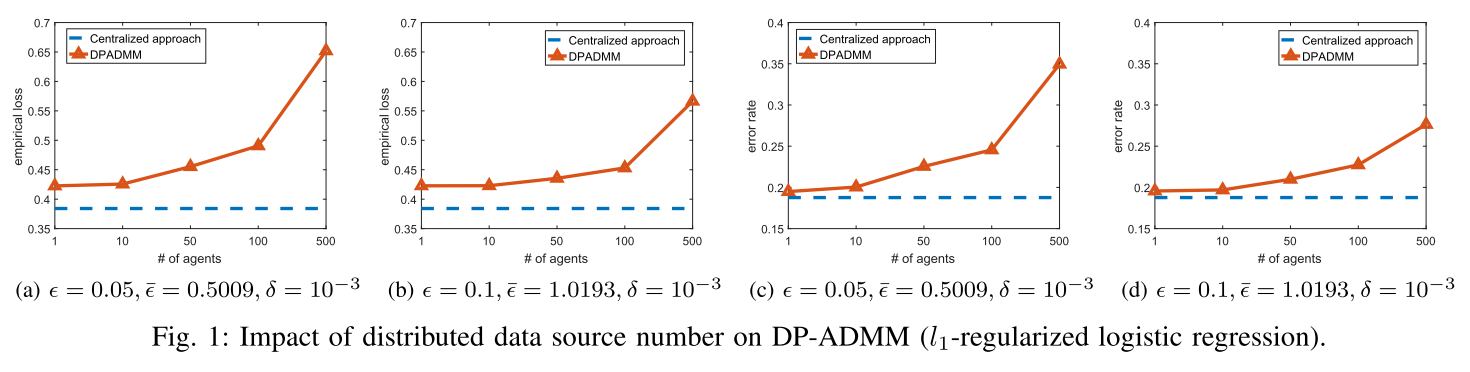
节点越多,效果越差,后面的实验节点数选了100。由于节点越多,每个节点可用的数据就越少,在保证同样隐私水平的情况下引入的噪声会越多,所以效果越差。(好像可以改进,想一下)
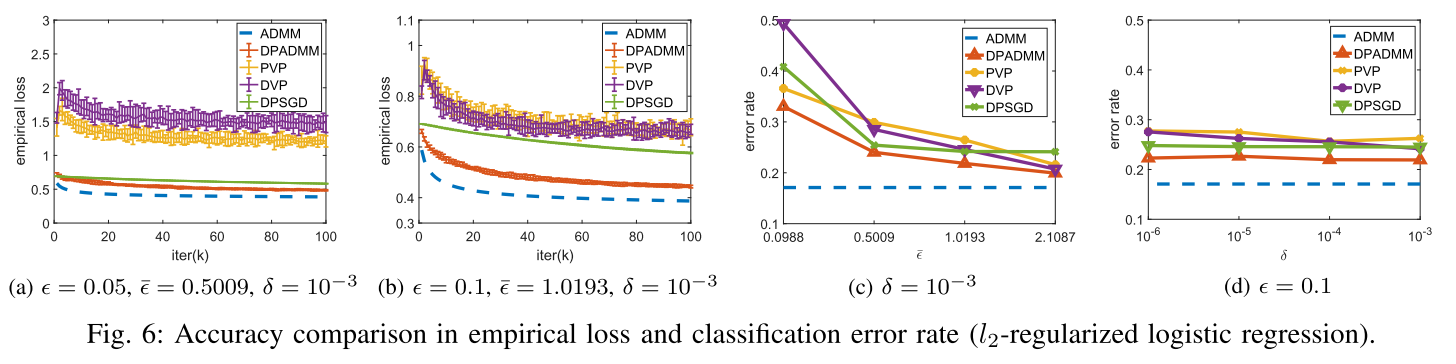
翻译原文:ADMM收敛最快,但是对噪声敏感。PVP、DVP效果不行。DPSGD对噪声不敏感但是收敛慢。我们的方法最吊。
Reference
[1] T. Zhang and Q. Zhu, “Dynamic differential privacy for admm-based distributed classification learning,” IEEE Transactions on Information Forensics and Security, vol. 12, no. 1, pp. 172–187, 2017.
[2] K. Chaudhuri, C. Monteleoni, and A. D. Sarwate, “Differentially private empirical risk minimization,” Journal of Machine Learning Research, vol. 12, no. Mar, pp. 1069–1109, 2011.
