Balle B, Wang Y X. Improving the gaussian mechanism for differential privacy: Analytical calibration and optimal denoising[J]. arXiv preprint arXiv:1805.06530, 2018.
提出了两种方法让bound更紧:
The first improvement is an algorithmic noise calibration strategy that uses numerical evaluations of the Gaussian cumulative density function (CDF) to obtain the optimal variance to achieve DP using Gaussian perturbation.
第一种是通过高斯的CDF来直接调整方差,以得到更优的高斯机制。
The second improvement equips the Gaussian perturbation mechanism with a post-processing step which denoises the output using adaptive estimation techniques from the statistics literature.
第二种用后处理的步骤,用统计学上的适应性估计技术对output降噪。
经典高斯机制的限制
经典高斯机制:$Z\sim N(0, \sigma^2)$, For any $\epsilon, \delta \in (0,1), \sigma = \Delta\sqrt{2\log(1.25/\delta)}/\epsilon$, 可以保证$(\epsilon,\delta)$-DP
很自然的两个疑问是:
a. 该$\sigma$取值在满足DP的前提下,是否保证是最小的噪声量
b. 当$\epsilon \ge 1$会发生什么。
这篇文章指出当$\epsilon \rightarrow 0$ (high privacy regime),$\sigma$是次优的。
而当$\varepsilon >1$时,
large values of $\varepsilon$ the standard deviation of a Gaussian perturbation that provides $(\varepsilon, \delta)$-DP must scale like $\Omega(1/\sqrt{\varepsilon})$.
-
Limitations in the High Privacy Regime

接下来会解释为什么经典高斯机制不能导出$\varepsilon \to 0$时的tight bounds,这也会说明定理2不是一个极端的例子,而是a fundamental limitation of trying to establish $(\varepsilon,\delta)$-DP through said sufficient condition.
-
Limitations of Privacy Loss Analyses
加一个服从高斯分布的噪声时,隐私损失也是服从高斯分布的[1]:
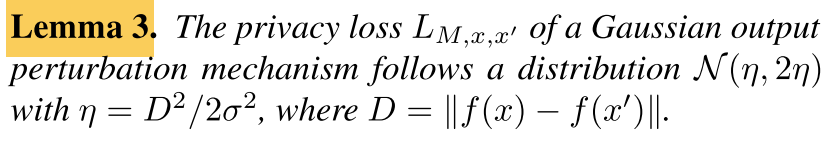
经典高斯机制的隐私分析需要以下条件:
a mechanism M is $(\varepsilon,\delta)$-DP if the privacy loss $L_{M,x,x’}$ satisfies
\[\forall x\simeq x': \mathbb{P}[L_{M,x,x' \ge \varepsilon}\leq \delta]\]引理3表明高斯机制的privacy loss也是一个高斯随机变量,对任何一对使得$f(x)\ne f(x’)$数据集,有$\mathbb{P}[L_{M,x,x’}>0]\ge 1/2$。这一点说明通常不可能用满足$(\varepsilon,\delta)$-DP的充分条件去证明高斯机制可以在任何$\delta<1/2$的情况下达到$(0,\delta)$-DP。也就是说,充分条件对于$\varepsilon \to 0$是不必要的。
(其实就是根据P[L] >= 1/2, 表明delta<1/2时不可能(0,delta)-DP的)
-
Limitations in the Low Privacy Regime
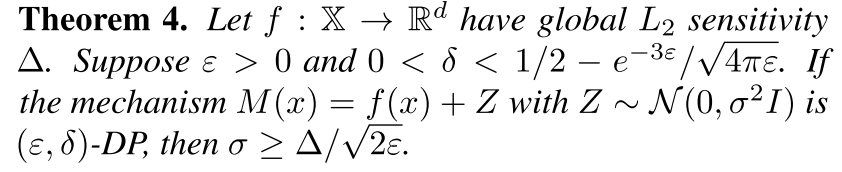
当$\varepsilon \to \infty$时,$\delta$会收敛到1/2.
This shows that the rate $\sigma = Θ(1/ε)$ provided by the classical Gaussian mechanism cannot be extended beyond the interval $\varepsilon \in (0, 1)$.
是说不能扩展到1以上么?
The Analytic Gausssian Mechanism
To do so we must address the two sources of slack in the classical analysis: the sufficient condition (2) used to reduce the analysis to finding an upper bound for $P[N(\eta, 2\eta) > \varepsilon]$, and the use of a Gaussian tail approximation to obtain such upper bound.

$\Phi$是标准正态分布的累积密度函数CDF。
因为L服从$N(\eta,2\eta), \eta=\frac{\Delta^2}{2\sigma^2}$, 所以$(L\cdot\frac{\sigma}{\Delta}-\frac{\Delta}{2\sigma}) \sim N(0,1)$。
$P[L\leq -\varepsilon]=P[(L\cdot\frac{\sigma}{\Delta}-\frac{\Delta}{2\sigma}) \leq (-\varepsilon\cdot\frac{\sigma}{\Delta}-\frac{\Delta}{2\sigma})]=\Phi(-\frac{\varepsilon\sigma}{\Delta}-\frac{\Delta}{2\sigma})$
继而根据引理7推导出定理8(引理7不截图了)。
定理8表明,为了得到一个满足$(\varepsilon,\delta)$-DP的输出扰动机制,需要使噪声的方差$\sigma^2$满足(6)式。
接下来就可以通过高斯分布的CDF的tail来推导$\sigma$的表达式,但是由于在非渐近状态下这些tail bounds的松弛(slack),将会导致次优结果。于是本文提出一种数值算法,利用高斯分布的CDF可以通过标准误差函数erf来表达($\Phi(t)=(1+erf(t/\sqrt{2}))/2$),来找出合适的$\sigma$。如算法1。

Optimal Denoising
是否可以对aGM的性能进行更进一步的优化?答案是yes and no。no是因为算法1已经对于给定的privacy budget给出了精确的噪声level $\sigma$。但是如果从另一个角度看,如何设计最优的DP机制M(x)来近似f(x),那么就还有可以改进的空间。
令$\hat{y}\sim N(f(x),\sigma^2I)$,目标是希望设计一种post-processing function $g$,使得$\tilde{y}=g(\hat{y})$比$\hat{y}$更接近于$f(x)$。
看不下去了。有需求再看。
2019.12.17 找到一个讲这篇的视频,贴几个slides截图。

除了趋近于0和大于1等条件,经典高斯机制不能满足外,在0和1之间,仍然可以做到更好。那么是什么原因造成的这一gap呢?

首先,privacy loss也是一个随机变量;其次是一个服从高斯分布$N(\eta,2\eta)$的随机变量($\eta = \frac{\Delta^2}{2\sigma^2}$);第三点可以看出$\delta$并不是tight bound。

给出了实际上的闭式解,因此需要等式右边满足定理才能保证$(\varepsilon,\delta)$-DP.

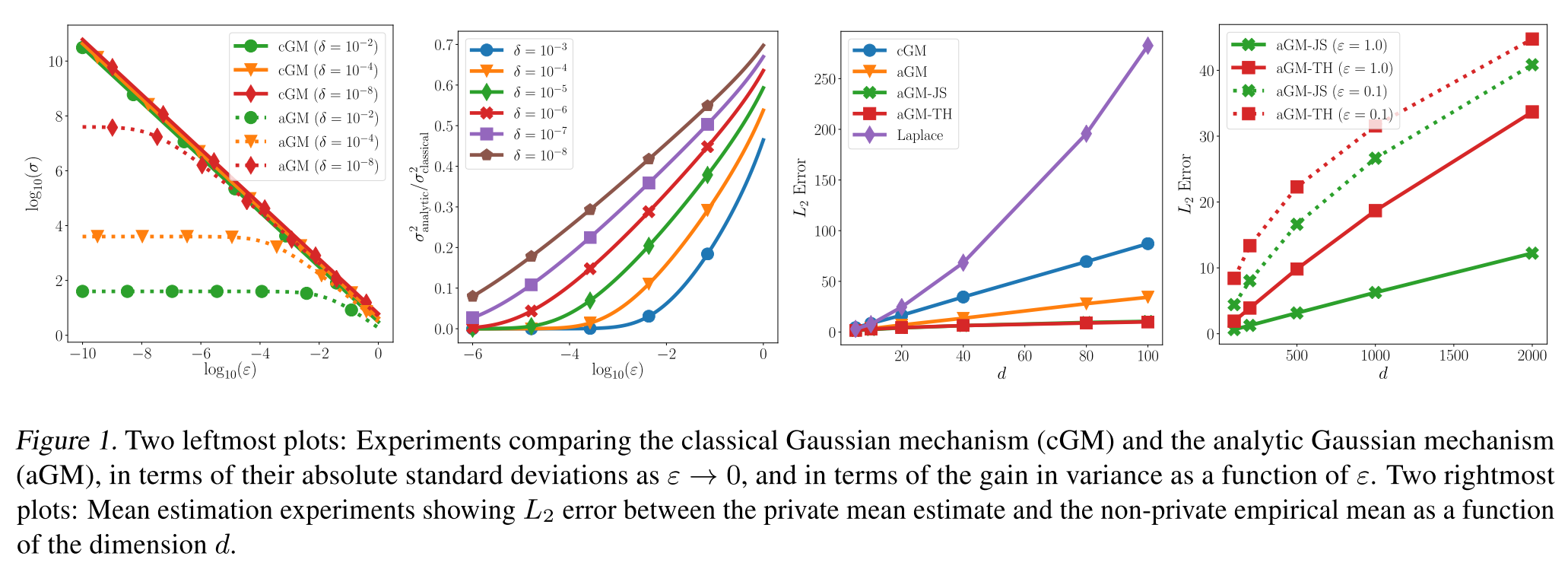
左侧俩表示$\varepsilon$取0到1时,analytic Gaussian mechanism和classical Gaussian mechanism的方差比较,可以看出前者的方差在$\varepsilon \to 0$时,比经典机制强好几个量级;当趋近于1时也强一点。
右侧的实验是求平均数(对应denoising部分),比较L2 error。

Conclusion
没有看完第4部分。
Problems for future work:
-
DP estimation问题。我们的后处理方法有效地将我们对算法的选择限制在隐私发布和后处理的组成上。 虽然我们现在知道我们在这两个方面都是最优的,但是我们还不清楚相对于最佳差分私有算法,我们是否会损失任何东西。
-
对于更为复杂的机制,是选择使用a) aGM with advanced composition[2] 还是b) Renyi DP[3] or zCDP[4] for tighter composition and calculate the $(\varepsilon,\delta)$ from moment bounds.
a对于为中间结果计算privacy参数更为tighter;b则在利用组合性质时更tighter,但是没有利用到aGM的优点。
Reference
[1] Dwork, C. and Rothblum, G. N. Concentrated differential privacy. arXiv preprint arXiv:1603.01887, 2016.
[2] Kairouz, P., Oh, S., and Viswanath, P. The composition theorem for differential privacy. In International Conference on Machine Learning (ICML), 2015.
[3] Mironov, I. Renyi differential privacy. In Computer Security Foundations Symposium (CSF), 2017 IEEE 30th, pp. 263– 275. IEEE, 2017.
[4] Bun, M. and Steinke, T. Concentrated differential privacy: Simplifications, extensions, and lower bounds. In The- ory ofCryptography Conference, pp. 635–658. Springer, 2016.
