Lee J, Kifer D. Concentrated differentially private gradient descent with adaptive per-iteration privacy budget[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2018: 1656-1665.
Introduction
这篇文章思路很巧妙,当时我也觉得在梯度上加入随机噪声,梯度方向一定会变来变去,加上之前做GBDT的那个实验,也有很不靠谱的时候,怎么就没有再往下想一下通过某些方法来保证梯度一定可以有效下降呢。。
传统的DP-SGD类算法有两个缺点:一是需要预先给出迭代次数T,如果T太小,可能算法还没有收敛到最优,如果T太大,那么每次迭代需要的$\epsilon_t$就会小,每次计算梯度引入到噪声量就会大,可能结果也不好;第二个是通常在优化的最开始,梯度是比较大的,这时少量噪声对梯度的影响就比较小,但随着迭代的进行梯度减小时,如果还是采用同样的噪声量,则对梯度的影响就会变大,可能影响收敛。
本文的方法就是在第t步时,计算noisy gradient $\tilde{S}_{t}=\nabla f\left(\mathbf{w}_{t}\right)+Y_{t}$;然后用剩下的隐私预算来选择t步时最优的step size。具体地,需要预先定义step size的集合$\Phi$(包括0),用differentially private noisy min algorithm[1]来近似地找到使$f\left(\mathbf{w}_{t}-\alpha \tilde{S}_{t}\right)$最小的$\alpha$,we find which step size causes the biggest decrease on the objective function。如果$\alpha$不为0,则$\mathbf{w}_{t+1}=\mathbf{w}_{t}-\alpha \tilde{S}_{t}$,通过不同的$\alpha$保证算法收敛更快;如果$\alpha$为0,则表明noise太大,会在接下来的迭代中增加privacy budget的分配,来减小noise。
Related Work
- output perturbation[2,3,4]:
[4] used algorithmic stability arguments to bound the L2 sensitivity of full batch gradient descent algorithm to determine the amount of noise that must be added to outputs that partially optimizes the objective function. Although they achieve theoretical near optimality, this algorithm has not been empirically shown to be superior to methods such as [2].
-
objective perturbation[2]提出了目标扰动的方案,用一种non-private optimization solver解决了这个问题。[9]通过放松了DP的方式(pureDP改成了$(\epsilon,\delta)$-DP)提高了utility。但是这种方案基于这个问题是可以精确求解的前提下,但是实际中,大部分优化问题都是近似解决的。
-
iterative gradient perturbation[5,6]和他们的变体[4,7,8]: [5] Bassily等人提出了$(\epsilon,\delta)$-DPSGD,在每一次迭代中,对梯度进行高斯噪声的扰动,用advanced组合性[10]和privacy amplification[11]来得到一个全部privacy loss的上界。
Further, they also have shown that their lower bounds on expected the excess risk is optimal, ignoring multiplicative log factor for both lipschitz convex and strongly convex functions.
[12] 针对Lasso问题优化了utility的下界。[7]借助了stochastic variance reduced gradient (SVRG) algorithm和梯度扰动结合,新的算法近似最优,且有更低的梯度复杂度。
[13] presented a genetic algorithm for differentially private model fitting, called PrivGene, which has a different flavor from other gradient-based methods. Given the fixed number oftotal iterations, at each iteration, PrivGene iteratively generates a set of candidates by emulating natural evolutions and chooses the one that best fits the model using the exponential mechanism [9].
以上所有算法都需要预先决定隐私预算。
Gradient Averaging For zCDP
本文算法很重要的一环就是如何回收利用对更新参数没有用的梯度估计。在第t次迭代中,分配$\rho_t$的隐私预算来扰动梯度,$S_t = \nabla f\left(\mathbf{w}_{t}\right)+N\left(0, \frac{\Delta_{2}(\nabla f)^{2}}{2 \rho_{t}}\right)$。
如果算法认定这个不够准确,就会在下一次迭代时分配隐私预算$\rho_{t+1}>\rho_{t}$。但是对于$S_t$,并不是直接丢弃,而是用$\rho_{t+1}-\rho_{t}$的隐私预算来计算 $S_{t}^{\prime}=\nabla f\left(\mathbf{w}{t}\right)+N\left(\mathbf{0}, \frac{\Delta{2}(\nabla f)^{2}}{2\left(\rho_{t+1}-\rho_{t}\right)}\right)$。
然后把$S_t$通过如下的方式组合起来:
\[\hat{S}_{t}=\frac{\rho_{t} S_{t}+\left(\rho_{t+1}-\rho_{t}\right) S_{t}^{\prime}}{\rho_{t}+\left(\rho_{t+1}-\rho_{t}\right)}\] \[E\left[\hat{S}_{t}\right]=\nabla f\left(\mathbf{w}_{t}\right)\] \[\begin{aligned} \operatorname{Var}\left(\hat{S}_{t}\right) &=\left(\rho_{t}^{2} \frac{\Delta_{2}(\nabla f)^{2}}{2 \rho_{t}}+\frac{\Delta_{2}(\nabla f)^{2}}{2\left(\rho_{t+1}-\rho_{t}\right)}\left(\rho_{t+1}-\rho_{t}\right)^{2}\right) / \rho_{t+1}^{2} \\ &=\frac{\Delta_{2}(\nabla f)^{2}}{2 \rho_{t+1}} \end{aligned}\]也就是说,先计算$S_t$,再计算$S_{t}^{\prime}$,最后得到$\hat{S}{t}$,一共使用了$\rho{t+1}$的隐私预算,产生答案的方差是$\frac{\Delta_{2}(\nabla f)^{2}}{2 \rho_{t+1}}$。仿佛没有消耗$\rho_t$一样。
Algorithm

算法2(DP-AGD,differentially private adaptive gradient descent algorithm)分为三个部分:
-
Private Gradient Approximation
用$\widetilde{\mathbf{g}}=\nabla f\left(\mathbf{w}{t}\right)+\mathcal{N}\left(0, \sigma^{2} \mathbf{I}\right)$计算梯度近似,噪声量$\sigma^2$取决于$\Delta_2(g)$。为了对这个敏感度进行bound,之前的工作[2,9]假设$|\mathbf{x}| \leq 1$,而本文对梯度进行了clip,计算梯度$\nabla \ell\left(\mathbf{w}{t} ; d_{i}\right)$ for $i=1, \ldots, n$,然后除以$\left(1, \frac{\left|\nabla \ell\left(\mathbf{w}{t} ; d{i}\right)\right|{2}}{C{\mathrm{grad}}}\right)$,求和,加入噪声$C_{\mathrm{grad}}^{2} / 2 \rho_{\mathrm{ng}}$,最后进行归一化处理。这样可以保证梯度的敏感度是$C_{\mathrm{grad}}$而且满足$\rho_{\mathrm{ng}}-\mathrm{ZCDP}$。
-
Step Size Selection
用$\rho_{nmax}$的隐私预算对$\widetilde{\boldsymbol{g}}{t}$进行测试,看梯度是否为下降方向。首先,算法构造了一个集合$\Omega=\left{f\left(\mathbf{w}{t}-\alpha \widetilde{\mathbf{g}}{t}\right) : \alpha \in \Phi\right}$,每个元素表示在$\mathbf{w}{t}-\alpha \widetilde{\mathbf{g}}_{t}$这个处的目标函数值,$\Phi$是一个预先定义的step size的集合。然后通过NoisyMax算法来决定哪个step size对应了最小的目标函数值。同样,为了对sensitivity进行bound,采用了clip的方式,但是并没有进行归一化,因为不会影响NoisyMax的结果。
$\Phi$的第一个元素设置为0,这样$\Omega$中始终包括当前的目标函数值$f\left(\mathbf{w}_{t}\right)$,$i$表示NoisyMax返回的index,如果$i>0$,就选择step size$\alpha_i$,如果$i=0$,表明当前梯度值不是下降方向。
-
Adaptive Noise Reduction
如果$-\widetilde{\mathbf{g}}{t}$不是一个下降方向,那么算法会在接下来的一次迭代中增加隐私预算,$\rho{\mathrm{ng}} \leftarrow(1+\gamma) \rho_{\mathrm{ng}}$,然后用$\rho_{\mathrm{ng}}-\rho_{\mathrm{old}}$的隐私预算重新计算梯度,直到NoisyMax返回一个表示下降方向的梯度index。
Experiments
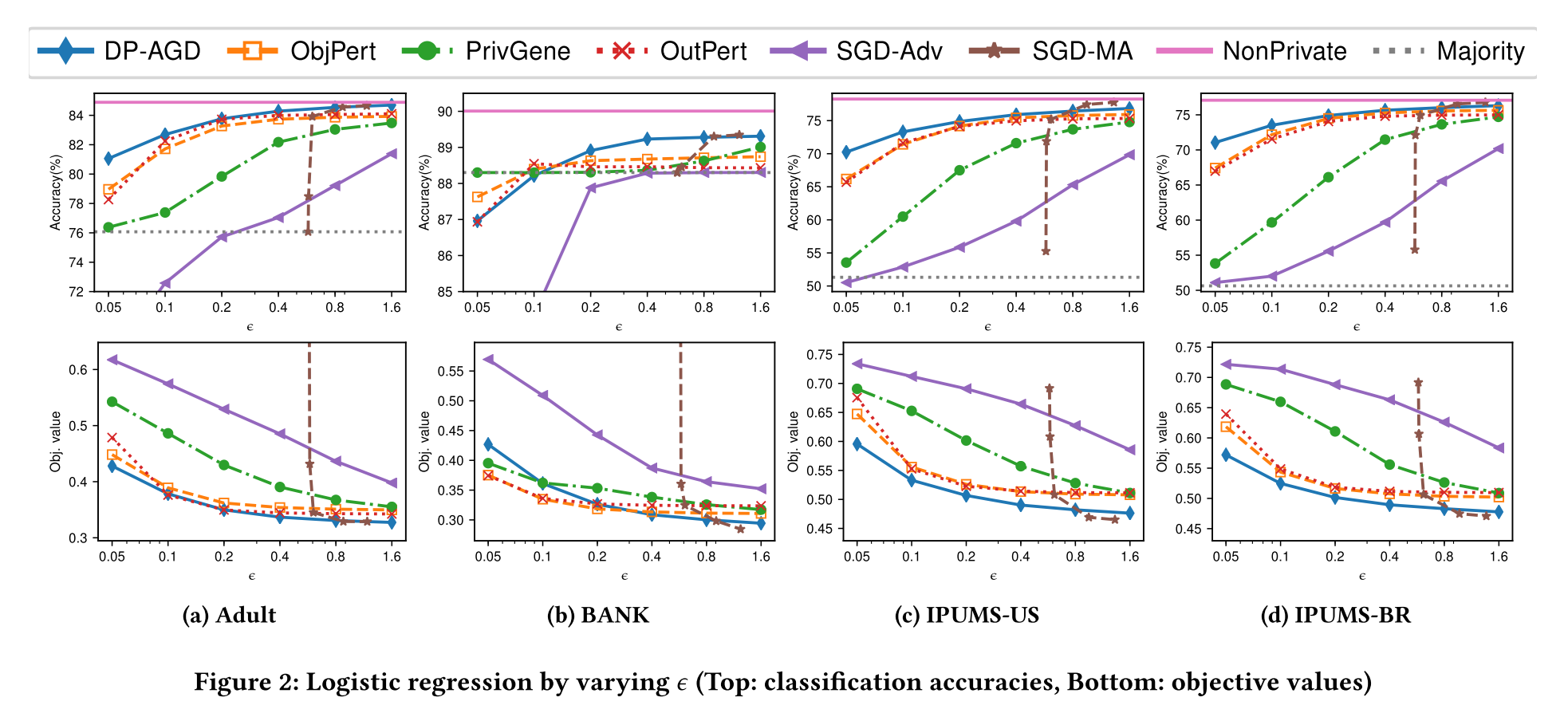
SGD-MA在$\epsilon>0.8$时效果很好,这是由于采用了moments accountant方案结合了由于subsampling产生的privacy amplification,使privacy loss的bound更紧,可以接受更多的迭代次数。但是在更严格的privacy区域表现并不好。
With δ fixed to 10−8, we empirically observe that, under the moments accountant, one single iteration of SGD update can incur the privacy cost of $\epsilon \approx 0.5756$. This renders the moments accountant method impractical when high level of privacy protection is required.
Reference
[1] Cynthia Dwork, Aaron Roth, et al. 2014. The algorithmic foundations of differ- ential privacy. Foundations and Trends® in Theoretical Computer Science 9, 3–4 (2014), 211–407.
[2] Kamalika Chaudhuri, Claire Monteleoni, and Anand D Sarwate. 2011. Differentially private empirical risk minimization. Journal ofMachine Learning Research 12, Mar (2011), 1069–1109
[3] Cynthia Dwork, Frank McSherry, Kobbi Nissim, and Adam Smith. 2006. Cali- brating noise to sensitivity in private data analysis. In Theory ofCryptography Conference. Springer, 265–284.
[4] Jiaqi Zhang, Kai Zheng, Wenlong Mou, and Liwei Wang. 2017. Efficient private ERM for smooth objectives. In Proceedings ofthe 26th International Joint Conference on Artificial Intelligence. AAAI Press, 3922–3928.
[5] Raef Bassily, Adam Smith, and Abhradeep Thakurta. 2014. Private Empirical Risk Minimization: Efficient Algorithms and Tight Error Bounds. In Proceedings ofthe 2014 IEEE 55th Annual Symposium on Foundations ofComputer Science (FOCS ’14). IEEE Computer Society, Washington, DC, USA, 464–473.
[6] Oliver Williams and Frank McSherry. 2010. Probabilistic inference and differential privacy. In Proceedings ofthe 23rd International Conference on Neural Information Processing Systems-Volume 2. Curran Associates Inc., 2451–2459
[7] Di Wang, Minwei Ye, and Jinhui Xu. 2017. Differentially Private Empirical Risk Minimization Revisited: Faster and More General. In Advances in Neural Information Processing Systems 30. Curran Associates, Inc., 2719–2728.
[8] Yu-Xiang Wang, Stephen Fienberg, and Alex Smola. 2015. Privacy for free: Posterior sampling and stochastic gradient monte carlo. In International Conference on Machine Learning. 2493–2502.
[9] Daniel Kifer, Adam Smith, and Abhradeep Thakurta. 2012. Private convex empirical risk minimization and high-dimensional regression. In Conference on Learning Theory. 25–1.
[10] C. Dwork, G. N. Rothblum, and S. Vadhan. 2010. Boosting and Differential Privacy. In 2010 IEEE 51st Annual Symposium on Foundations ofComputer Science. 51–60.
[11] Amos Beimel, Hai Brenner, Shiva Prasad Kasiviswanathan, and Kobbi Nissim. 2014. Bounds on the sample complexity for private learning and private data release. Machine learning 94, 3 (2014), 401–437.
[12] Kunal Talwar, Abhradeep Guha Thakurta, and Li Zhang. 2015. Nearly optimal private lasso. In Advances in Neural Information Processing Systems. 3025–3033.
[13] Jun Zhang, Xiaokui Xiao, Yin Yang, Zhenjie Zhang, and Marianne Winslett. 2013. PrivGene: Differentially Private Model Fitting Using Genetic Algorithms. In Proceedings ofthe 2013 ACMSIGMOD International Conference on Management of Data (SIGMOD ’13). ACM, New York, NY, USA, 665–676.
