DP-ERM系列一：Privacy preserving logistic regression notes

Background

先引用一下知乎大佬[2]的线性分类模型泄漏什么隐私？

首先简单说说线性分类模型的隐私泄露问题。最为直观地，在一维情况下，线性分类器会返回样本的中位数，而中位数通常是一个具体样本的取值，那么这个样本的即被暴露给了获得模型的使用者，我们认为这侵犯到了他的隐私。在高维情况下依然存在相似的情况。具体见发表于SODA13的The Power of Linear Reconstruction Attacks一文。

我们期望得到一类在差分隐私框架下的机器学习模型A，使得原先的机器学习模型具有隐私保护能力。具体而言，即一类经验误差最小化模型，再具体而言…一类线性核的经验误差最小化模型(Logistic Regression/SVM/Least squares…)

大神Kamalika Chaudhuri这一系列的开坑之作，发表在nips2008和jmlr2011上。主要思路就是Output Perturbation和Objective Perturbation。

在背景介绍里提到[1]虽然加更少的噪声（smoothed-sensitivity）就可以保护隐私，但是某个函数的smoothed sensitivity比较难计算。

A Simple Algorithm (Output Perturbation)

上述算法可以很容易地看出，在输出上直接加入了来自Gamma分布的噪声。

\[w^* = \arg\min_w \frac{1}{n}\sum_{i=1}^n l(w, (x_i,y_i))+\frac{1}{2}\Vert w\Vert^2\]

$w^{priv}=w^*+b, b\sim \Gamma(d,\frac{2}{n\lambda})$ (d应该是x的维度？b是个向量，是每个都不一样还是一组一样大小的元素？)

以上主要给出sensitivity的大小。

参考[2]，给出计算sensitivity的过程。

\[G(w) = J(w,D)=\frac{1}{n}\sum_{i=1}^n l(w,(x_i,y_i))+\frac{\lambda}{2}\Vert w \Vert^2\] \[g(w)=\frac{1}{n}(l(y'_n, w^Tx'_n)-l(y_n, w^Tx_n)), J(w,D')=G(w)+g(w)\] \[\Delta_{\arg\min}=\Vert \arg\min_w G(w)-\arg\min_w (G+g)(w) = \Vert w_1-w_2 \Vert\] \[\nabla G(w_1)=\nabla G(w_2)+\nabla g(w_2)=0\]

$G(w)$是$\lambda$-强凸的，因此$(\nabla G(w_1)-\nabla G(w_2))^T(w_1-w_2) \geq \lambda\Vert w_1-w_2 \Vert^2$

\[\Vert w_1-w_2 \Vert\cdot\Vert\nabla g(w_2)\Vert \geq (w_1-w_2)^T \nabla g(w_2)\geq \lambda\Vert w_1-w_2\Vert^2\]

所以$\Vert w_1-w_2 \Vert\leq \frac{1}{\lambda}\max_w \nabla\Vert g(w) \Vert$

$\nabla g(w)=\frac{1}{n}(y_n l'(y_n w^Tx_n)x_n - y'_n l'(y'_n w^Tx'_n)x'_n)$ (有点不确定？)

又因为$\vert l’\vert\leq 1, \Vert x\Vert\leq 1, \vert y\vert \leq 1$,所以$\Vert\nabla g(w)\Vert \leq \frac{2}{n}$, $\Delta_{\arg\min} \leq\frac{2}{n\lambda}$.

这个是性能 (learning performance) 差距的bound。

A New Algorithm (Objective Perturbation)

同样需要$\Vert x_i \Vert \leq 1$。这个$b$也是个向量？是一堆一样大小的噪声还是每个大小不一样？

We observe that our method solves a convex programming problem very similar to the logistic regression convex program, and therefore it has running time similar to that of logistic regression.

算法2解决了一个凸规划问题，和lr很像。相当于是针对目标函数的扰动。

上面这个算法2 [3]来自同样作者的JMLR2011，

\[J(w)=\frac{1}{n}\sum_{i=1}^n l(w, (x_i,y_i))+\frac{\lambda}{2}\Vert w\Vert^2\]

$w^{priv}=\arg\min J(w)+ \frac{1}{n}w^Tb$ ([2]中这里应该是少了$\frac{1}{n}$)

where $b\sim e^{-\frac{\epsilon’}{2}\Vert b \Vert}, \epsilon’=\epsilon-\log((1+\frac{c}{n\lambda})^2)$.

(吐槽一下：同一个作者写的论文，为什么要在两篇上搞出不同的符号，不能按照约定俗成的来吗。。)

The algorithm requires a certain slack in the privacy parameter. This is due to additional factors in bounding the ratio of the densities.

为了证明算法2满足$\epsilon$-DP，需要针对loss function做较强的假设。$l(\cdot)$是强凸的且二次可微，$\vert l’(\cdot)\vert\leq 1,\vert l’’(\cdot)\vert\leq c$, 知乎大牛[2]中，对于logistic regression，$c=\frac{1}{4}$。

为了求$w^{priv}$，令$\nabla J(w)+b = 0$，也就是说，在给定数据集$D$的情况下，$b$和$w^{priv}$是一一对应的。

$b=-n\lambda w-\sum_{i=1}^{n} y_i l'(y_i(w^{priv})^T x_i)x_i$,

\[\frac{Pr[w^{priv}\vert D]}{Pr[w^{priv}\vert D']}=\frac{Pr[b\vert D]}{Pr[b'\vert D']}\cdot\frac{\vert\det(Jacobi(w^{priv}\rightarrow b\vert D))\vert^{-1}}{\vert\det(Jacobi(w^{priv}\rightarrow b'\vert D'))\vert^{-1}},\]

令

\[A=n\lambda I_d+\sum_{i=1}^{n}y_i^2 l''(y_i(w^{priv})^Tx_i)x_ix_i^T\] \[E=-y_n^2l''(y_n(w^{priv})^Tx_n)x_nx_n^T+(y'_n)^2l''(y'_n(w^{priv})^Tx'_n)x'_n x_{n}^{'T}\] \[Jacobi(w^{priv}\rightarrow b\vert D)=-A\]

$Jacobi(w^{priv}\rightarrow b\vert D')=-(A+E)$ (没懂)

令$\lambda_1(M)$和$\lambda_2(M)$分别表示矩阵M的最大的和第二大的特征值。

\[\frac{\vert\det(Jacobi(w^{priv}\rightarrow b\vert D'))\vert}{\vert\det(Jacobi(w^{priv}\rightarrow b\vert D))\vert}=\frac{ \vert\det(A+E)\vert}{\vert\det A\vert}=\vert 1+\lambda_1(A^{-1}E)+\lambda_2(A^{-1}E)+\lambda_1(A^{-1}E)\lambda_2(A^{-1}E)\vert.\]

对于$j=1,2$，有$\vert\lambda_j(A^{-1}E)\vert \leq \frac{\vert\lambda_j(E)\vert}{n\lambda}$,

根据三角不等式，
$\left|\lambda_{1}(E)\right|+\left|\lambda_{2}(E)\right| \leq\left|y_{n}^{2} \ell^{\prime \prime}\left(y_{n} ({w}^{priv})^{T} \mathbf{x}_{n}\right)\right| \cdot\left\|\mathbf{x}_{n}\right\|+\left|-\left(y_{n}^{\prime}\right)^{2} \ell^{\prime \prime}\left(y_{n}^{\prime} ({w}^{priv})^{T} \mathbf{x}_{n}^{\prime}\right)\right| \cdot\left\|\mathbf{x}_{n}^{\prime}\right\|$

然后根据假设中的bound，
$\left|\lambda_{1}(E)\right|+\left|\lambda_{2}(E)\right| \leq 2 c$

\[\frac{\vert\det(A+E)\vert}{\vert\operatorname{det}(A)\vert} \leq (1+\frac{c}{n\lambda})^2\] \[b-b^{\prime}=y_{n} \ell^{\prime}\left(y_{n}\left(w^{p r i v}\right)^{T} x_{n}\right) x_{n}-y_{n}^{\prime} \ell^{\prime}\left(y_{n}^{\prime}\left(w^{p r i v}\right)^{T} x_{n}^{\prime}\right) x_{n}^{\prime}\] \[\Vert{b}\Vert-\Vert b^{\prime}\Vert \leq \Vert b-b^{\prime}\Vert \leq 2\] \[\frac{\operatorname{Pr}[b \vert D]}{\operatorname{Pr}\left[b \vert D^{\prime}\right]} \leq e^{\epsilon^{\prime}\left(\Vert b\Vert-\left\Vert b^{\prime}\right\Vert \right) / 2} \leq e^{\epsilon^{\prime}}\] \[\frac{\operatorname{Pr}\left[w^{p r i v} \vert D\right]}{\operatorname{Pr}\left[w^{p r i v} \vert D^{\prime}\right]} \leq e^{\epsilon^{\prime}} \cdot\left(1+\frac{c}{n \lambda}\right)^{2}=e^{\epsilon}\]

因此，在目标函数中对参数进行扰动满足$\epsilon$-DP。

目标扰动方法并不基于函数的敏感度，而是通过一个巧妙的方法建立起了随机噪声与输出之间的对应关系，从而实现输出的随机性，形成满足差分隐私的隐私保护算法。这样的方式非常地亮眼，但很可惜地是后来也没有类似的构建随机性的dpERM方法（暂未读到）。

最后，满足一定条件的凸优化问题都可以用这种方法来解决：

Experiments

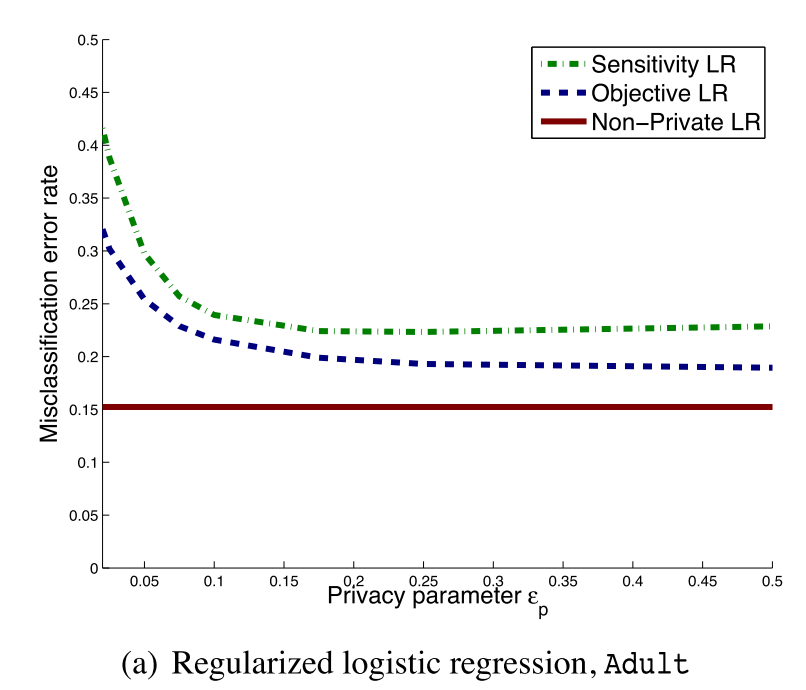
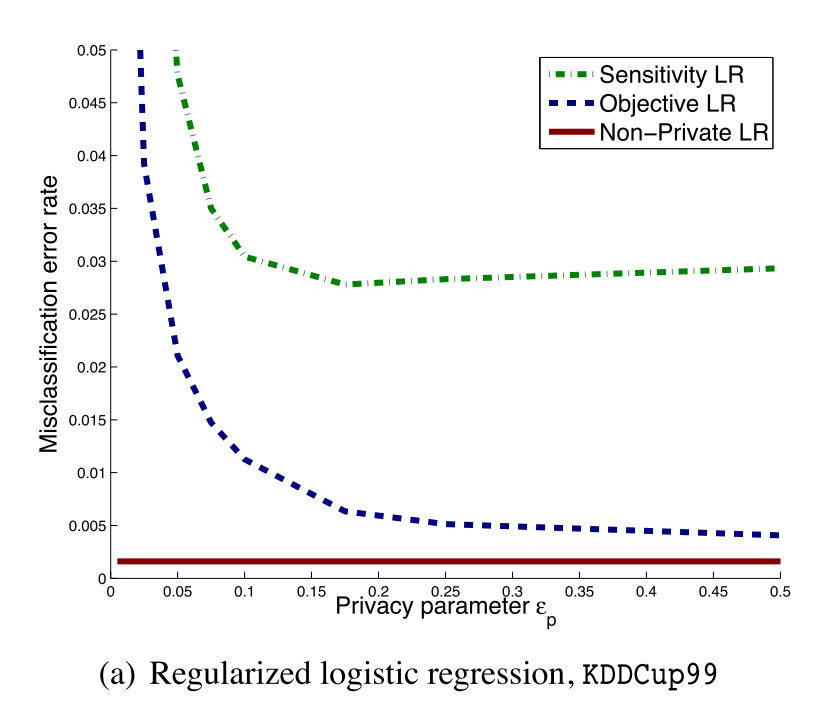
可以看出，目标扰动方法全面优于输出扰动方法。

这两组试验结果，上面的是Adult数据集的，下面的是kdd cup99的数据集。两者的$\epsilon=0.1$。

比较了不同正则项参数下的模型准确度变化。其中比较有意思的一点是，对于privateERM来说，正则项的增大帮助了提高模型性能。在表中可以看到Non-Private方法在正则项增大的情况下很早就达到了准确度峰值，之后随正则项增加，准确度是降低的，这也是比较符合我们的认识的。但对于privateERM，随着正则项参数的增大，峰值姗姗来迟，这一点可以这么来解释：正则项是有利于形成隐私保护的。最直接地，对于输出扰动，正则项越大，模型的输出受限越大，敏感度越低则噪声越小[2]。

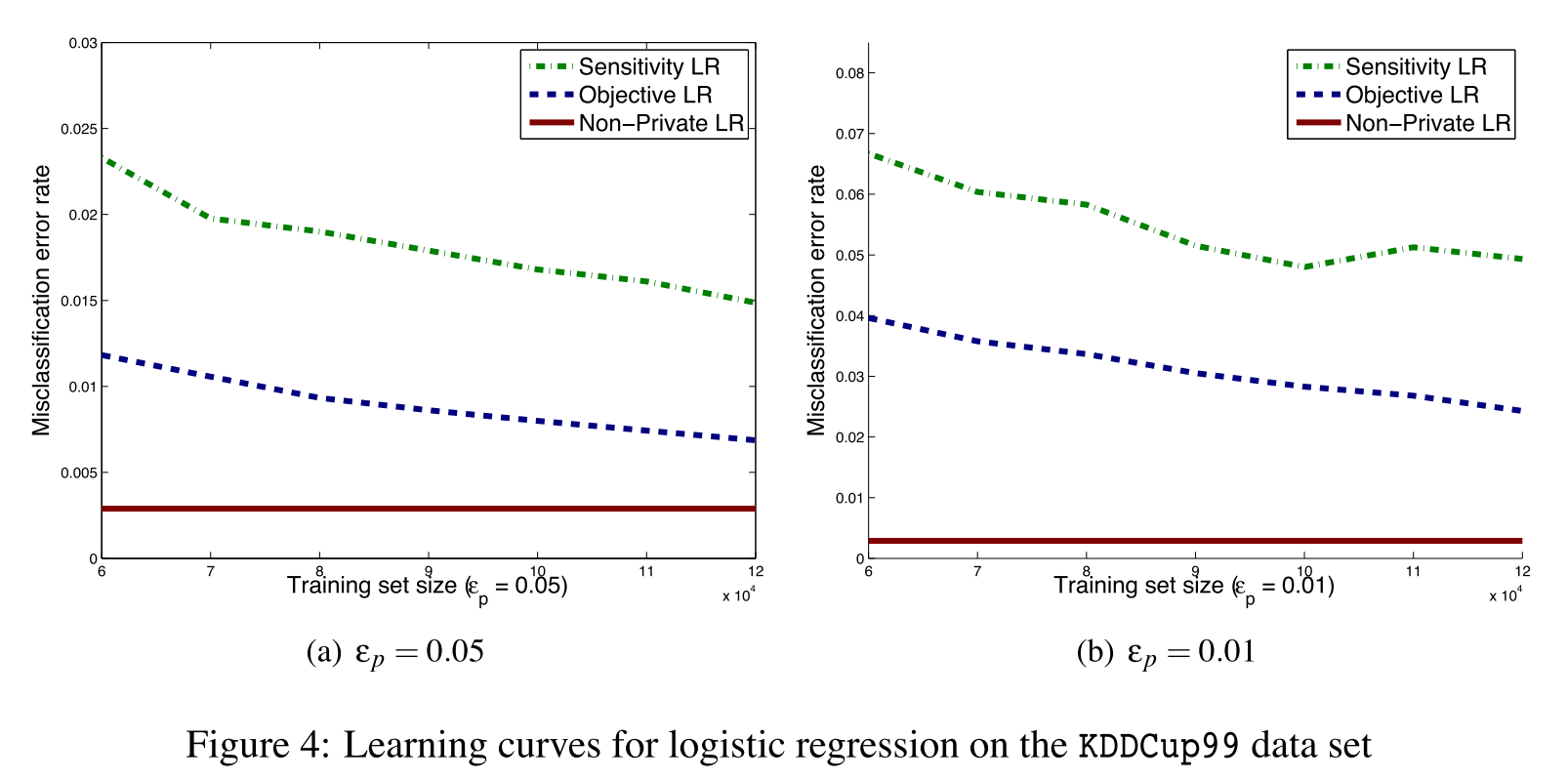
上图表明随着数据量的增加，private算法可以继续提高准确度。

Reference

[1] K. Nissim, S. Raskhodnikova, and A. Smith. Smooth sensitivity and sampling in private data analysis. In D. S. Johnson and U. Feige, editors, STOC, pages 75–84. ACM, 2007.

[2] 满足差分隐私的经验误差最小化方法

[3] Chaudhuri K, Monteleoni C, Sarwate A D. Differentially private empirical risk minimization[J]. Journal of Machine Learning Research, 2011, 12(Mar): 1069-1109.

Questions

如果$J(w)$不是强凸或者可微的呢？二次可微？