Mishra N, Thakurta A. (Nearly) optimal differentially private stochastic multi-arm bandits[C]//Proceedings of the Thirty-First Conference on Uncertainty in Artificial Intelligence. AUAI Press, 2015: 592-601.
Introduction
UAI 2015的文章,主要是针对UCB算法和TS算法进行了隐私保护,声称达到了接近于non-private版本算法的效果(较低的regret)。
在motivation中提到了practical的一点,是说在广告点击中,可以获得点击广告的反馈,而未点击的候选广告则没有任何反馈,而bandit learning的方式正适用于这一点,且有良好的理论保证。(这就很practical了?)
Tree based aggregation
[1,2]中介绍了基于树的聚合方法。树聚合的方法可以用于处理流数据,对于一个数据集$D = {f_1,\dots,f_T}$,每个时刻只有一个$f_t \in [0,1]$到达。在时刻t,该机制输出$v_t=\sum_{\tau=1}^t f_\tau$并保证输出序列${f_1,\dots,f_T}$满足$\epsilon$-DP。
One can design an algorithm (using a binary tree based aggregation), which assures an additive error of $O(\frac{\log^{1.5}T}{\epsilon})$ per query.
Moreover, it can be extended to the case where $f_t \in \mathbb{R}^p$ and $\Vert f_t \Vert _2 \leq 1$ for all $t \in [T]$.
可以扩展。
Private UCB Sampling
UCB的regret bound是$O(\log T)$的。
每个arm对应的reward总值$r_a(t)$只依赖于我们想要保护的数据集,因此只要保证了$r_a(t) \ \ t\in[T]$ 序列的隐私性就可以保证整个算法的隐私性,也就是只要每个arm满足$\epsilon/k$-DP,整个算法就满足$\epsilon$-DP。

Additionally, to counter the noise added to the empirical mean, we loosen the confidence interval for the biases of each arm.
从算法1中可以看出,在第4和12行将每次获取的reward值$f_t(a_t)$通过基于树的聚合机制实现了隐私保护。在第7行,为了“counter the noise added to the empirical mean”,加入了这个数值用来放松每个arm的置信区间。
Privacy Guarantee
k个arm,维护k棵树,每棵树保证是$\epsilon/k$-DP,整个算法就满足$\epsilon$-DP。
Utility Guarantee

整个算法的regret可以由$\mathbb{E}[\sum_{a \in C: \mu_a < \mu_a^* } \Delta_a n_a(T)]$给出,其中$\Delta_a = \mu_a^*-\mu_a$。首先通过计算整个reward总值中被加入的噪声量的bound,然后用这个bound可以表明次优的arm被选的次数很少。然后通过分析次优arm的exploration and exploitation阶段,表明在$O(\frac{k\log^2T \log(kT)}{\epsilon\Delta^2})$轮的选择后,就大概率不会再被选了。(这种方法主要是按照non-private UCB sampling [3]来分析的)。
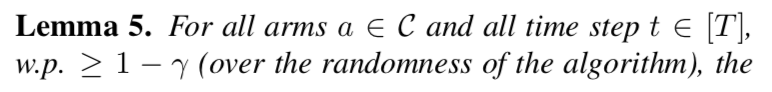
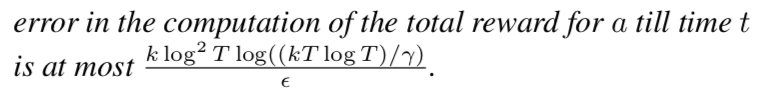
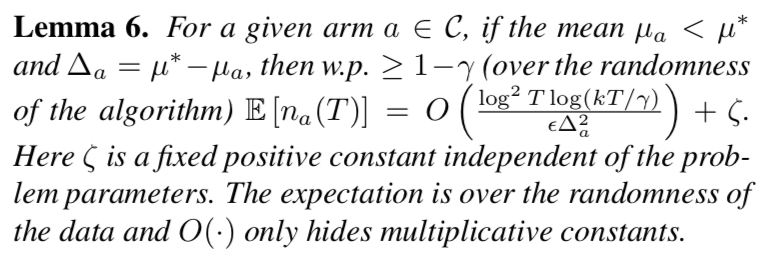
Private Thompson Sampling
尽管TS算法在20世纪早期就被提出,但是[4]才首次对TS算法进行了regret分析,表明是对数相关于次数T的。本文继续研究private TS算法的动机是,在non-private版本中,TS的性能比UCB好很多。
TS算法的基本思想也比较简单,对于$k$个arms来说,在时刻$t$,记$r_{a_1}(t),\dots,r_{a_k}(t)$是每个arm得到奖励的次数,$n_{a_1}(t),\dots,n_{a_k}(t)$是相应arm被pull的总数,选arm的规则是,从beta分布$\theta_i\sim Beta(r_{a_i}(t)+1, n_{a_i}(t)-r_{a_i}(t)+1)$中选出最高的$\theta_i$。[4]给出了该算法的regret是$O(\sum_{a\in C-a^} (\frac{1}{\Delta_a^2})^2 \log T)$,其中$a^$是最优的arm,$\Delta_a=\mu_{a^*}-\mu_a$。
在MAB问题中,如果某个arm在最开始表现不好,那么它就很难在被pull,所以它的经验均值要比真实均值小。
One interesting observation in the MAB problems is that all the sequential algorithms would encourage a downward bias, which means that if an arm does not give good results initially then it will not be pulled again, therefore it’s empirical mean would be much lower than its true mean.
UCB算法通过向经验均值添加pull次数($n_a(t)$)的单调递减函数来解决该问题。
But in case of Thompson sampling, we are randomizing our decision hence the bias correction mechanism is different, it is due to randomization. In Thompson sampling, the biggest challenge is to bound the number of mistakes in the initial rounds.Moreover to ensure differential privacy, we introduce additional randomness to the original Thompson sampling algorithm, it becomes even harder for us to analyze the number of mistakes in the initial rounds.
因此,本文采取了不同的方法,将算法分成了明确的exploration阶段和exploration & exploitation阶段。前者的思想是估计两个arm的偏差(在足够的置信度下)而不理会犯了错误的数量。后者用标准的TS算法,除了保证rewards是满足DP条件下获取的。

可以看出算法2分为三部分,第一部分是对$\Delta$的估计,
Notice that in the first part, each arm i, $i\in[k]$ is pulled in batches of m-pulls, till the condition in Line 8 in Algorithm 2 is satisfied. If each of this batch is made $\epsilon/2k$-differentially private, then by parallel composition property of differential privacy, the first phase is $\epsilon/2$-differentially private.
这里有点奇怪,每个arm是$\epsilon/2k$的话,k个arm按照并行组合性怎么还需要加起来呢?算法第5行加入的是$Lap(\frac{2k}{\epsilon m})$的噪声量。第9行如果$T \leq \tau$怎么办(regret分析给出了答案)?如果T不知道怎么办?
接下来需要随机pull一定次数来build confidence。用private trees来保证隐私。
最后是混合阶段,同样用树来保证隐私。15行中的$f$是什么?
Regret Analysis
Moreover, we argue that the gap estimation runs for at most poly $\log T$ number of rounds.
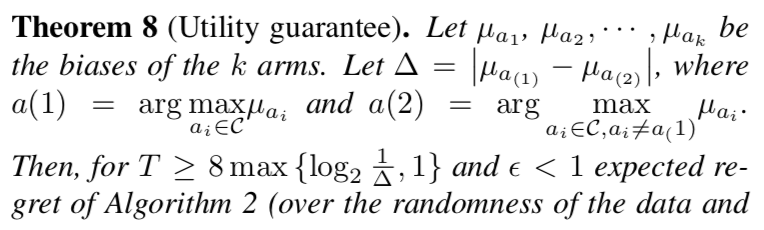



Reference
[1] TH Hubert Chan, Elaine Shi, and Dawn Song. Private and continual release of statistics. In ICALP. 2010
[2] Cynthia Dwork, Moni Naor, Omer Reingold, Guy Roth- blum, and Salil Vadhan. On the complexity of differentially private data release: efficient algorithms and hardness re- sults. In STOC, pages 381–390, 2009.
[3] Kamalika Chaudhuri. Topics in online learning: Lecture notes. 2011.
[4] Shipra Agrawal and Navin Goyal. Analysis of thompson sampling for the multi-armed bandit problem. In COLT, 2012.
