混淆电路(Garbled Circuits)
Yao大佬在1986年提出的。可以叫多方安全计算的基石。
主要思想是离散的、fixed-size function可以转化为逻辑门电路,如果有一种可以安全地计算这个电路的方法,那么就可以安全地计算对应的function。
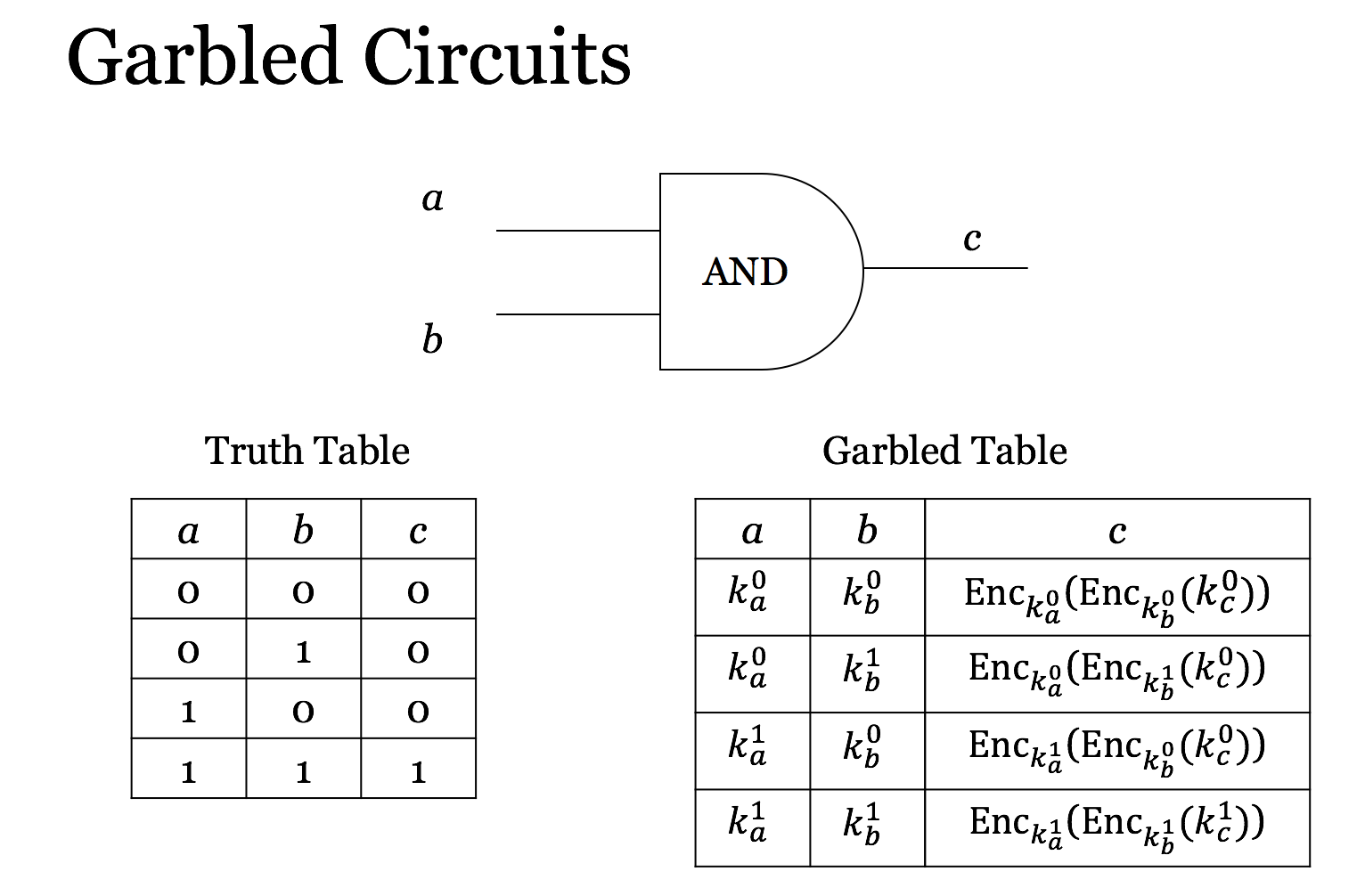
以AND function(与门)为例,实际上可以看成是一张真值表,如上图所示,两个输入同为1时,输出才为1;否则输出为0。
目标是用一种加密方式,可以达到不知道输入(a,b)并且不知道输出(c)的情况下,仍然可以计算这个门电路,并且把输出作为下一个门电路的输入。
具体协议是,a和b对应的两条输入线,每条线有0和1两个可能的值,a首先给每条线指定两个随机的key,分别对应0和1,也就是$k_a^0, k_a^1$和$k_b^0, k_b^1$。
然后加密生成如图右侧的Garbled Table(实际上叫加密表更为合适,因为没有打乱顺序)。
a接下来打乱上表的顺序,然后将GT和自己输入对应的key发送给b,比如,a的输入是0,那就发$k_a^0$ ,输入是1就发$k_a^1$。同时要将$k_b^0, k_b^1$也发送给b。
但是这样就会产生一个问题,b有了上述key以后就可以解密出至少两个输出,这样会有问题。所以需要用到Oblivious Transfer notes中提到的OT协议,让a把两个key加密后$E(k_b^0), E(k_b^1)$发送给b,b通过这个协议只能解密出一个有效的key,从而使a不知道自己使用的是哪个key。
接下来b将解密得到的$k_c^?$发给Alice,Alice通过对比是$k_c^0$还是$k_c^1$得知计算结果是0还是1。由于整个过程大家收发的都是密文或随机数,所以没有有效信息泄露。
以上是GC中最简单的一个门电路的思想,这样可以在不暴露两方输入的情况下,得到输出。加法和乘法作为计算最基本的单位,需要多个门电路组合运算,实际情况会比这个复杂很多,也有很多工作就是在做这方面的优化。有了加法和乘法,自然就可以通过安全地两方计算来实现更复杂的算法,这方面的工作也有很多,尤其是现在机器学习大火,但是数据却可能带来隐私问题的情况下。
