转载自知乎专栏:FOLLOW THE REGULARIZED LEADER (FTRL) 算法总结
之前主要关注FTRL,没有仔细的看过FTRL之前的文章,这里简单记一下,以后翻出来看也方便。
FTRL是Google从2010到2013护的坑,从理论到工程实现,对处理如Logistic Regression之类的带非光滑正则项的凸优化问题上性能出色(L1范数,控制模型复杂度和稀疏化)。
问题描述(最小化目标函数)
-
约束优化(convex constraint formulation)
\[\hat{w} = \arg\min_{w} \sum_{i=1}^{n} L(w, z_i) \text{ subject to } ||w||_1 \leq s\] -
无约束优化(soft regularization formulation)
\[\hat{w} = \arg\min_{w} \sum_{i=1}^{n} L(w, z_i) + \lambda ||w||_1\]
上述二者在选择合适的$\lambda$时是等价的
损失函数
-
线性回归
\(h(W, X_j) = W^T X_j\) 损失函数为$L(W,Z) = \sum_j (y_j - W^T X_j)$
-
逻辑回归
\(h(W, X_j) = \frac{1}{1+\exp(-W^T X_j)}\) 损失函数为$L(W,Z) = \sum_j \log(1+\exp(-y_j W^T X_j))$
1. Truncate Gradient
截断梯度法(TG, Truncated Gradient)是由John Langford,Lihong Li 和 Tong Zhang 在2009年提出,对简单截断的一种改进。
1)L1正则化法
由于L1正则项在0处不可导,往往会造成平滑的凸优化问题变成非平滑凸优化问题,因此在每次迭代中采用次梯度计算L1正则项的梯度。
\[W_{(t+1)}=W_{(t)}-\eta^{(t)}G^{(t)}-\eta^{(t)}\lambda sgn(W^{t})\]2)简单截断法
简单粗暴,以k为窗口,如果t/k不为整数时,按照标准的SGD处理;如果为整数,则
\[W^{(t+1)}=T_{0}(W^{(t)}-\eta^{(t)}G^{(t)},\theta),\]其中$T_{0}(v_{i},\theta)=0 \text{ if } \vert v_{i} \vert \leq \theta, T_{0}(v_{i},\theta)=v_{i} \text{ otherwise}.$
就是小于某个阈值的w直接设置为0.
3)截断梯度法(Truncated Gradient)
同样是以k为窗口,当t/k不为整数时,$\lambda^{(t)} = 0$;当为整数时,$\lambda^{(t)} = k \lambda$
\[W^{(t+1)}=T_{1}(W^{(t)}-\eta^{(t)}G^{(t)},\eta^{(t)}\lambda^{(t)},\theta),\]其中$T_{1}(v_{i},\alpha,\theta)=\max(0,v_{i}-\alpha) \text{ if } v_{i}\in [0,\theta], $
$T_{1}(v_{i},\alpha,\theta)=\min(0,v_{i}+\alpha) \text{ else if } v_{i}\in [-\theta,0), $
$T_{1}(v_{i},\alpha,\theta)=v_{i} \text{ otherwise },$
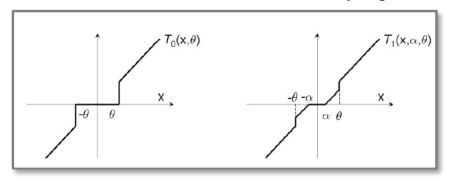
从图中可以看出,TG和简单截断当区别就是多了一个$\alpha$.
2. FOBOS (Forward Backward Splitting)
1)前向后向切分(FOBOS,Forward Backward Splitting)是 John Duchi 和 Yoran Singer 提出的。在该算法中,权重的更新分成两个步骤:
\[W^{(t+0.5)}=W^{(t)}-\eta^{(t)}G^{(t)},\] \[W^{(t+1)}=argmin_{W}\{\frac{1}{2}||W-W^{(t+0.5)}||_{2}^{2}+\eta^{(t+0.5)}\Psi(W)\}.\]第一个步骤实际上是一个标准的梯度下降(SGD),第二个步骤是对第一个步骤的结果进行局部调整。写成一个公式那就是:
\[W^{(t+1)}=argmin_{W}\{\frac{1}{2}||W-W^{(t)}+\eta^{(t)}G^{(t)}||_{2}^{2}+\eta^{(t+0.5)}\Psi(W)\}.\]假设 $F(W)=\frac{1}{2} \Vert W-W^{(t)}+\eta^{(t)}G^{(t)} \Vert_{2}^{2}+\eta^{(t+0.5)}\Psi(W)$,如果$W^{(t+1)}$存在一个最优解,那么可以推断$0$向量一定属于$F(W)$的次梯度集合:
\[0 \in \partial F(W)=W-W^{(t)}+\eta^{(t)}G^{(t)}+\eta^{(t+0.5)}\partial\Psi(W).\]因为$W^{(t+1)}=argmin_{W}F(W)$,那么可以得到权重更新的另外一种形式:
\[W^{(t+1)}=W^{(t)}-\eta^{(t)}G^{(t)}-\eta^{(t+0.5)}\partial \Psi(W^{(t+1)}).\]从上面的公式可以看出,更新后的$W^{(t+1)}$不仅和$W^{(t)}$有关,还和自己$\Psi(W^{(t+1)})$有关。这也许就是“前向后向切分”这个名称的由来。
2)FOBOS(Forward Backward Splitting)的 L1 正则化
假设$\Psi(W)$是L1范数,中间向量是$W^{(t+0.5)}=(v_{1},…,v_{N})\in\mathbb{R}^{N}$,并且参数$\tilde{\lambda}=\eta^{(t+0.5)}\lambda,$,那么公式就可以展开得到
\[W^{(t+1)}=argmin_{W}\{\frac{1}{2}||W-W^{(t+0.5)}||_{2}^{2}+\eta^{(t+0.5)}\Psi(W)\}\] \[=argmin_{W}\sum_{i=1}^{N}(\frac{1}{2}(w_{i}-v_{i})^{2}+\tilde{\lambda}|w_{i}|).\]所以,可以对特征权重$W$的每一个维度进行单独求解:
\[w^{(t+1)}_{i}=argmin_{w_{i}}\bigg(\frac{1}{2}(w_{i}-v_{i})^{2}+\tilde{\lambda}|w_{i}|\bigg) \text{ for all } 1\leq i \leq N.\]Claim. 如果\(w_{i}^{*}\)是\(\min_{w_{i}}\bigg(\frac{1}{2}(w_{i}-v_{i})^{2}+\tilde{\lambda} \vert w_{i}\vert\bigg)\)的最优解,那么\(w_{i}^{*}v_{i}\geq 0.\)
证明:反证法,如果\(w_{i}^{*}v_{i} < 0\),那么\(\frac{1}{2}v_{i}^{2}<\frac{1}{2}(w_{i}^{*}-v_{i})^{2}+\tilde{\lambda} \vert w_{i}^{*} \vert\),这与条件矛盾。
通过数学计算可以证明:在L1正则化下,FOBOS 的特征权重的各个维度的更新公式是:
\[w_{i}^{(t+1)}=sgn(v_{i})\max(0,|v_{i}|-\tilde{\lambda})\] \[= sgn(w_{i}^{(t)}-\eta^{(t)}g_{i}^{(t)})\max\{0,|w_{i}^{(t)}-\eta^{(t)}g_{i}^{(t)}|-\eta^{(t+0.5)}\lambda\} \text{ for all }1\leq i \leq N,\]其中$g_i^{(t)}$是梯度在$G^{(t)}$第$i$个维度的分量。
从公式上看,如果$\vert w_{i}^{(t)}-\eta^{(t)}g_{i}^{(t)} \vert \leq\eta^{(t+0.5)}\lambda,$,则有$w_{i}^{(t+1)}=0$. 意思就是如果这次训练产生梯度的变化不足以令权重值发生足够大的变化时,就认为在这次训练中该维度不够重要,应该强制其权重是$0$.
如果$\vert w_{i}^{(t)}-\eta^{(t)}g_{i}^{(t)} \vert \geq\eta^{(t+0.5)}\lambda$,那么则有
\[w_{i}^{(t+1)}=(w_{i}^{(t)}-\eta^{(t)}g_{i}^{(t)})-\eta^{(t+0.5)}\lambda \cdot sgn(w_{i}^{(t)}-\eta^{(t)}g_{i}^{(t)}).\]3)L1-FOBOS和TG的关系
令$\theta=+\infty, k=1, \lambda_{TG}^{(t)}=\eta^{(t+0.5)}\lambda$,可以得到 L1-FOBOS 与 Truncated Gradient 完全一致,换句话说 L1-FOBOS 是 Truncated Gradient 在一些特定条件下的形式。
3. RDA(Regularized Dual Averaging Algorithm)
1) RDA(Regularized Dual Averaging Algorithm)叫做正则对偶平均算法,特征权重的更新策略是:
\[W^{(t+1)}= \arg\min_{W} \bigg\{\frac{1}{t}\sum_{r=1}^{t}G^{(r)}\cdot W + \Psi(W) +\frac{\beta^{(t)}}{t}h(W)\bigg\},\]其中$G^{(t)} \cdot W$指的是内积,$\Psi(W)$是正则项,$h(W)$是一个严格凸函数,${\beta^{(t)} \vert t\geq 1}$是一个非负递增序列。
从公式中可以看出:
- $\frac{1}{t}\sum_{r=1}^{t}G^{(r)}\cdot W$包括了之前所有梯度的平均值。
- 具有正则项$\Psi(W)$。
- 额外项$\frac{\beta^{(t)}}{t}h(W)$。
2) RDA的L1正则化
假设$ \Psi(W)= \Vert W \Vert_{1}, h(W)=\frac{1}{2} \Vert W \Vert_{2}^{2};$ i.e. $h(W)$是一个严格凸函数;$\beta^{(t)}=\gamma\sqrt{t} \text{ with } \gamma>0$是一个非负递增序列。那么 RDA 算法就可以写成:
\[W^{(t+1)}=argmin_{W}\bigg\{\frac{1}{t}\sum_{r=1}^{t}G^{(r)}\cdot W + \lambda||W||_{1}+\frac{\gamma}{2\sqrt{t}}||W||_{2}^{2}\bigg\}.\]此时可以采取同样的策略,把各个维度拆分成N个独立的问题来处理。也就是:
\[w_{i+1}^{(t+1)}=argmin_{w_{i}}\bigg\{\overline{g}_{i}^{(t)}+\lambda|w_{i}|+\frac{\gamma}{2\sqrt{t}}w_{i}^{2}\bigg\},\]其中,\(\lambda>0, \gamma>0, \overline{g}_{i}^{(t)}=\frac{1}{t} \sum_{r=1}^{t}g_{i}^{(r)}.\)
通过数学推导可以证明:
\[w_{i}^{(t+1)}=0, \text{ if } | \overline{g}_{i}^{(t)} |<\lambda,\] \[w_{i}^{(t+1)}=-\frac{\sqrt{t}}{\gamma}\bigg(\overline{g}_{i}^{(t)}-\lambda\cdot sgn(\overline{g}_{i}^{(t)})\bigg), \text{ otherwise}.\]意思就是:当某个维度的累加平均值$\vert \overline{g}_{i}^{(t)}\vert$小于$\lambda$时,该维度的权重被设置成零,此时就可以产生特征权重的稀疏性。
3) L1-RDA和L1-FOBOS对比
从截断方式来看,在 RDA 的算法中,只要梯度的累加平均值小于参数$\lambda$,就直接进行截断,说明 RDA 更容易产生稀疏性;同时,RDA 中截断的条件是考虑梯度的累加平均值,可以避免因为某些维度训练不足而导致截断的问题,这一点与 TG,FOBOS 不一样。通过调节参数$\lambda$,可以在精度和稀疏性上进行权衡。
4. FTRL (Follow The Regularized Leader)
FTRL 算法综合考虑了 FOBOS 和 RDA 对于梯度和正则项的优势和不足,其特征权重的更新公式是:
\[W^{(t+1)}=argmin_{W}\bigg\{G^{(1:t)}\cdot W+\lambda_{1}||W||_{1}+\frac{\lambda_{2}}{2}||W||_{2}^{2}+\frac{1}{2}\sum_{s=1}^{t}\sigma^{(s)}||W-W^{(s)}||_{2}^{2}\bigg\}.\]上面的公式出现了L2范数,不过这一项的引入不会影响 FTRL 的稀疏性,只是使得求解结果更加“平滑”。通过数学计算并且放弃常数项可以得到上面的优化问题相当于求使得下面式子的最小的参数$W$:
\[(G^{(1:t)}-\sum_{s=1}^{t}\sigma^{(s)}W^{(s)})\cdot W + \lambda_{1}||W||_{1}+\frac{1}{2}(\lambda_{2}+\sum_{s=1}^{t}\sigma^{(s)})||W||_{2}^{2}.\]如果假设 \(Z^{(t)}=G^{(1:t)}-\sum_{s=1}^{t}\sigma^{(s)}W^{(s)}=Z^{(t-1)}+G^{(t)}-\sigma^{(t)}W^{(t)},\) 上式等价于
\[W^{(t+1)}=argmin_{W}\bigg\{Z^{(t)}\cdot W + \lambda_{1}||W||_{1}+\frac{1}{2}(\lambda_{2}+\sum_{s=1}^{t}\sigma^{(s)})||W||_{2}^{2}\bigg\}.\]写成分量的形式就是:
\[argmin_{w_{i}}\bigg\{z_{i}^{(t)}w_{i}+\lambda_{1}|w_{i}|+\frac{1}{2}(\lambda_{2}+\sum_{s=1}^{t}\sigma^{(s)})w_{i}^{2}\bigg\}.\]通过计算可以直接得到:
\[w_{i}^{(t+1)}=0, \text{ if } |z_{i}^{(t)}|<\lambda_{1},\] \[w_{i}^{(t+1)}=-(\lambda_{2}+\sum_{s=1}^{t}\sigma^{(s)})^{-1}\cdot(z_{i}^{(t)}-\lambda_{1}\cdot sgn(z_{i}^{(t)})), \text{ otherwise.}\]由此可以证明:引入 L2 正则化并没有对 FTRL 的稀疏性产生影响。
