Mohassel P, Zhang Y. Secureml: A system for scalable privacy-preserving machine learning[C]//2017 IEEE Symposium on Security and Privacy (SP). IEEE, 2017: 19-38.
Abstract
本论文在特定计算场景下实现了安全多方计算的优化。针对线性回归、逻辑回归、神经网络训练问题,本论文给出了优化方案,并通过理论证明和实际验证说明了方案的可行性。
在两个不会合作的server模型上实现的协议。
Our protocols fall in the two-server model where data owners distribute their private data among two non-colluding servers who train various models on the joint data using secure two-party computation. We develop new techniques to support secure arithmetic operations on shared decimal numbers, and propose MPC-friendly alternatives to non-linear functions such as sigmoid and softmax that are superior to prior work.
Introduction
- 本文聚焦于two server model。将MPC缩减到了2PC,极大的提高了效率。
- 在模型训练期间,users可以是offline的。
- 也可以用在两个server联合训练模型的场景,也是十分常见的。
Related Work
Contributions
- 为线性回归、逻辑回归、神经网络提出了新的协议
- 综合使用了Secret sharing and arithmetic with precomputed triplets + Garbled circuit。
- 从实现角度讲
- 系统比以前的工作快了54~1270倍。
- 扩展性:100w数据,5000 features的逻辑回归。
Preliminaries
Secure Computation
-
Oblivious Transfer. OT是一种常被用在MPC中的加密原语。在OT协议中,发送者S有两个输入$x_0, x_1$,接收者R有选择位b,想不泄漏b给S的情况下获取到$x_b$。本文用OT在offline协议中来生成乘法三元组;在online阶段为LR和神经网络训练,安全地计算激活函数。
本文的OT用了[correlated OT extension][1],其中发送者的两个输入是相关的:一个随机值$s_0$和$s_1 = f(s_0)$。COT的通信:$l$-bit messages,需要$\lambda + l$ bits,计算包括3次哈希。
-
Garbled Circuit 2PC [混淆电路][2]包括带有随机种子$\sigma$的混淆算法和一个函数$f$,生成混淆电路$F$和解码表(decoding table)$dec$;编码算法(encoding algorithm)将$x$和随机种子$\sigma$作为输入生成混淆输入$\hat{x}$;评估算法(evaluation algorithm)将$\hat{x}$和$F$作为输入,返回混淆的输出$\hat{z}$;最后,解码算法(decoding algorithm)将$dec$和$\hat{z}$作为输入,返回$f(x)$.
接下来就可以设计一个安全的两方通信协议:Alice生成随机种子$\sigma$,为函数$f$运行混淆算法得到混淆电路$GC$;利用$\sigma$,将输入$x$编码成$\hat{x}$。 Alice把$\hat{x}$和$GC$发给Bob。 Bob利用OT将输入$y$的每一位编码得到$\hat{y}$。运行评估算法,输入为$GC$,$\hat{x}$,$\hat{y}$,得到garbled output $\hat{z}$。 接下来
We can have Alice, Bob, or both learn an output by communicating the decoding table accordingly.The above protocol securely realizes the ideal functionality $F_f$ that simply takes the parties inputs and computes $f$ on them.
- Secret Sharing and Multiplication Triplets. 所有中间数据的传输都是secret-shared。有三种:Additive sharing, Boolean sharing and Yao sharing. [3]中是详细的介绍。
Privacy-Preserving Linear Regression
很直观的想法就是利用上述Secret Sharing 和 arithmetic with precomputed triplets对SGD进行安全地计算:
SGD: $w_i = w_i - \alpha(\mathbb{x} \cdot \mathbb{w} - y) x_i$
Users secret share data and values (x,y)
Servers initialize and secret share the model w
Run SGD using pre-computed multiplication triplets
但是有一个问题,Secret Sharing只针对整数有效,而SGD则需要通过小数计算。
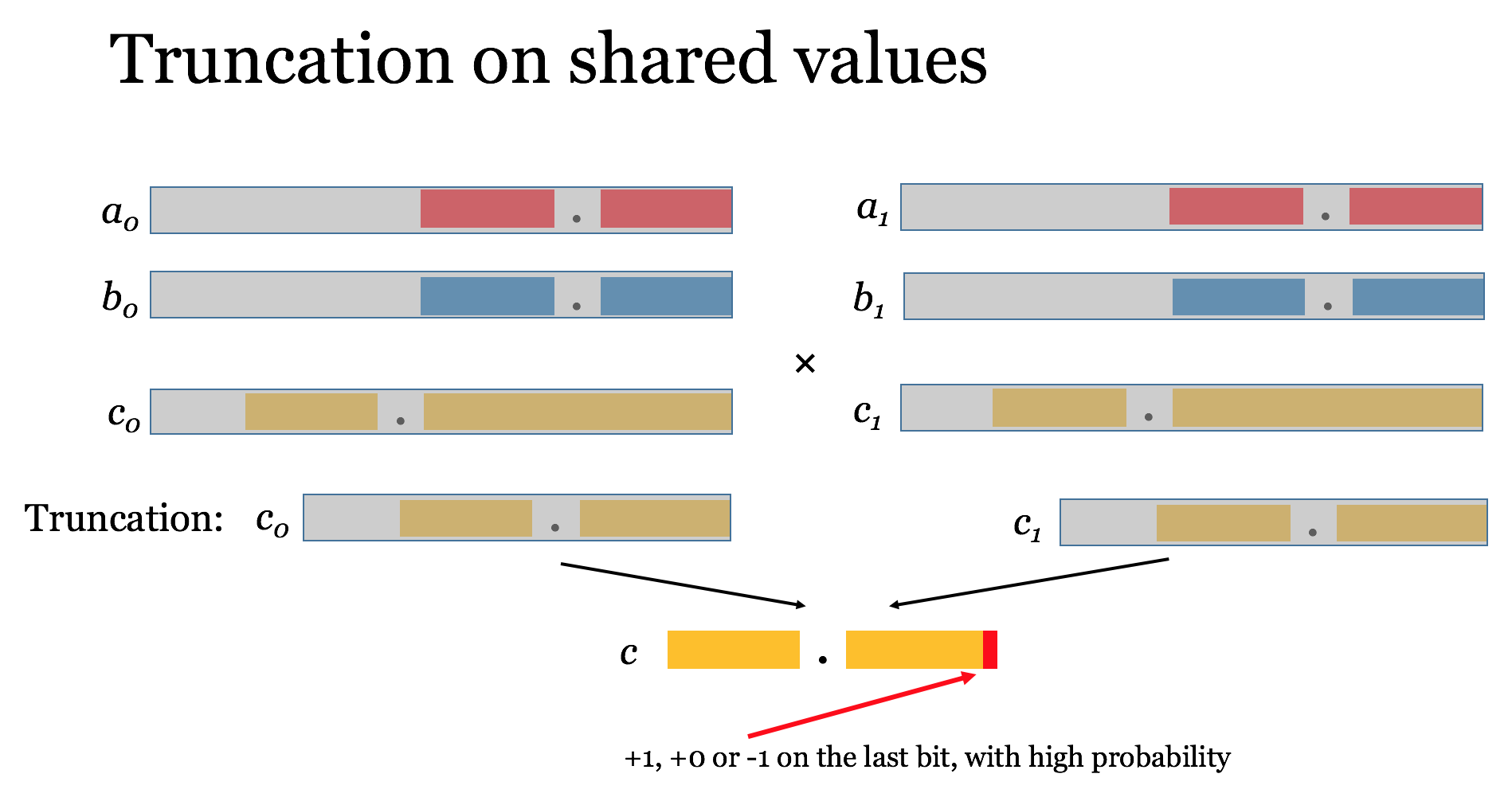
直接计算小数部分,然后截断。因此加入第4步就是完整的安全计算SGD方法。
- Truncate the shares after every multiplication
Privacy Preserving Logistic Regression
对于逻辑回归,由于sigmod函数$f(u) = \frac{1}{1+\exp(-u)}$计算需要除法和乘方,利用2PC for arithmetic or boolean circuit是难以实现的。文献[4]采用了多项式近似的方法,但是要high-degree polynomial才能比较准确(比如10)。但通常为了有效性,会采用2或者3来计算,误差较大。因此本文设计了新的激活函数。
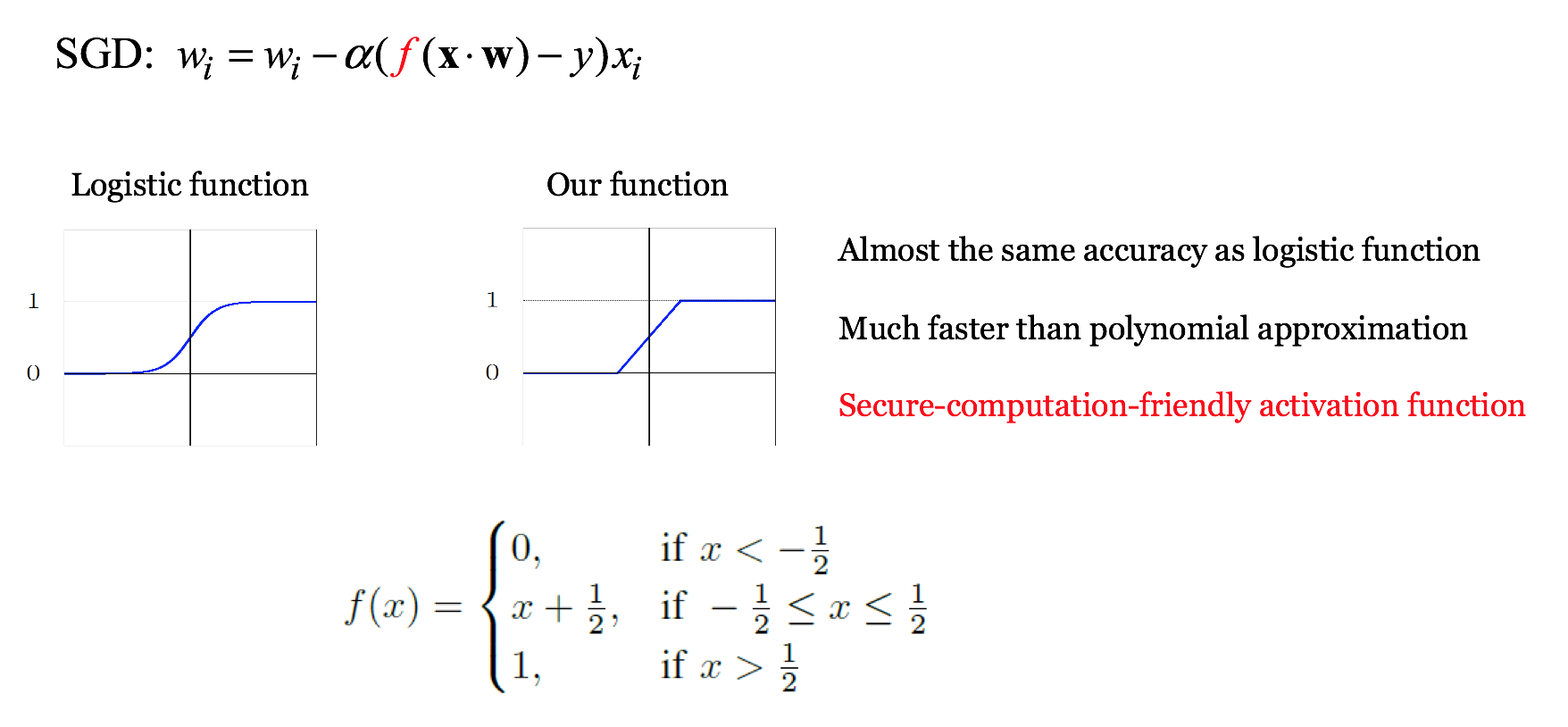
Reference
[1] Asharov G, Lindell Y, Schneider T, et al. More efficient oblivious transfer and extensions for faster secure computation[C]//Proceedings of the 2013 ACM SIGSAC conference on Computer & communications security. ACM, 2013: 535-548.
[2] Yao A C C. Protocols for secure computations[C]//FOCS. 1982, 82: 160-164.
[3] Demmler D, Schneider T, Zohner M. ABY-A Framework for Efficient Mixed-Protocol Secure Two-Party Computation[C]//NDSS. 2015.
[4] Scalable and Secure Logistic Regression via Homomorphic Encryption
结论
有点不想看了。就是大概了解一下目前OT和GC怎么用,细节还是挺难看的。。主要和目前研究的东西不太相关,需要的话等有空再补坑吧。
